Balancing rotating masses
For machines to run smoothly without vibration it is necessary for all the rotating masses to be in a state of balance.

Balancing co-planar masses (static balance)
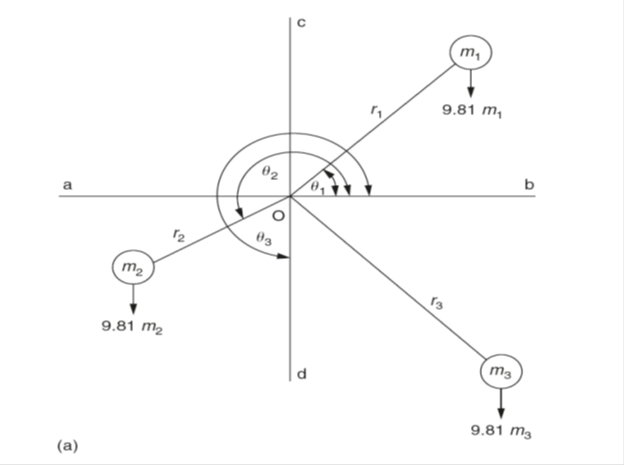
Co-planar masses refer to masses that lie in the same plane. For a body to be in static equilibrium there must be no resultant force or moment acting on the body. The algebraic sum of the moments must equal zero. Figure 1 (a) shows three co-planar masses positioned about a point O. For all practical purposes on planet earth the gravitational forces acting on the masses will be 9.81 × mass in each instance.

For the system of masses shown to be balanced it must be in equilibrium and, therefore, the algebraic sum of the moments about the centre of rotation O must be zero. This can be expressed mathematically as:

9.81 m₁r₁ cos θ₁ + 9.81 m₂r₂ cos θ₂ + 9.81 m₃r₃ cos θ₃ = 0

Dividing through by 9.81 it becomes:
m₁r₁ cos θ₁ + m₂r₂ cos θ₂ + m₃r₃ cos θ₃ = 0

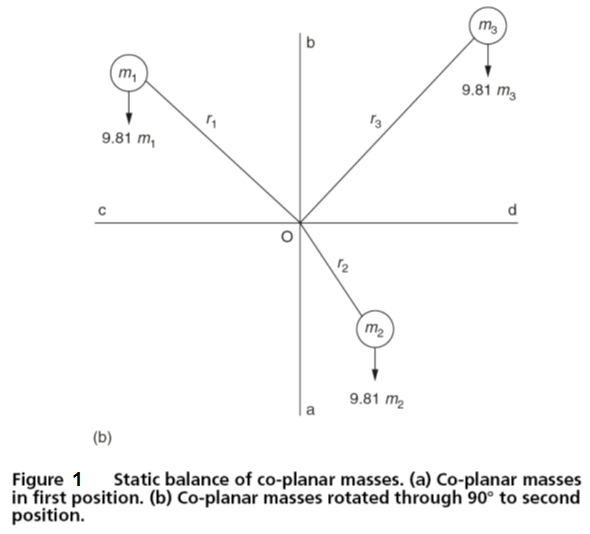
However this single expression is insufficient for the system of masses to be balanced for all angular positions. The system now has to be rotated through 90° as shown in Fig. 3.12(b) and the algebraic sum of the moments about O must be again be zero.

9.81 m₁r₁ sin θ₁ + 9.81 m₂r₂ sin θ₂ + 9.81 m₃r₃ sin θ₃ = 0

Again dividing through by 9.81 it becomes:
m₁r₁ sin θ₁ + m₂r₂ sin θ₂ + m₃r₃ sin θ₃ = 0

If the system is in balance for any two positions at right angles, it will also be in balance for any intermediate positions. Therefore the foregoing equations enable the balance of a system to be checked. If the system is out of balance then the same equations enable the magnitude and position of a balancing mass to be determined.

Balancing co-planar masses (dynamic balance)
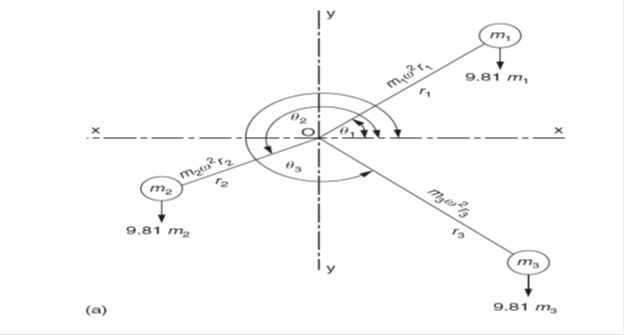
The subject of dynamic balancing is highly complex and an in depth treatment will not be attempted in this pocket book as there is insufficient space. However, a simple system of co-planar forces rotating about a point O will be considered, Fig.1(a) shows such a system. When they are rotating, each of the masses exerts a centrifugal force of mr ω ² on the point O (an axis or shaft). The rotational speed ω is expressed in rad/s. As previously, the algebraic sum of the moments about the point O must equal zero in two directions at right angles (x and y) as shown in Fig. 1(a).

Therefore the two equations applying to dynamic balance are:

m₁r₁ ω ² cos θ₁ + m₂r₂ ω ² cos θ₂ + m₃r₃ ω ² cos θ₃ = 0 and
m₁r₁ ω ² sin θ₁ + m₂r₂ ω ² sin θ₂ + m₃r₃ ω ² sin θ₃ = 0

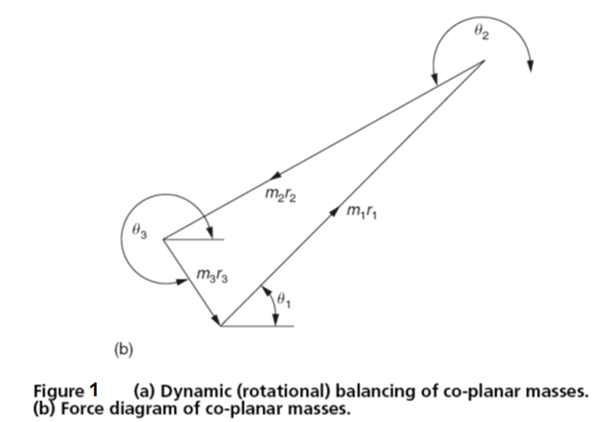
Dividing through by ω², which is a constant for any given speed of rotation, the equations become identical to the previous ones for static balance. Therefore for any system of co-planar forces the conditions for static and dynamic balance are the same and independent of the speed of rotation. Figure 1(b) shows the vector diagram of forces representing the previous equations.

• If the diagram is closed as shown, then the masses are in balance.
• If the diagram does not close then the masses are not in balance and the closing vector gives the angular position and the mr value of the mass required to achieve balance in the system.