Acceleration due to gravity at the surface of the Earth

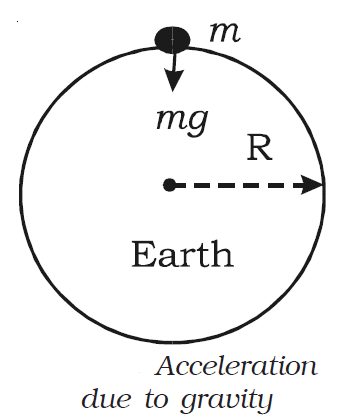
Consider a body of mass m on the surface of the Earth as shown in the diagram below. Its distance from the centre of the Earth is R (radius of the Earth).

The gravitational force experienced by the body is F = GMm/R^2 where M is the mass of the Earth. From Newton’s second law of motion, Force F = mg.
Equating the above two forces, GMm/R^2 = mg
∴ g = GM/R^2

This equation shows that g is independent of the mass of the body m. But, it varies with the distance from the centre of the Earth. If the Earth is assumed to be a sphere of radius R, the value of g on the surface of the Earth is given by g = GM/R^2

Mass of the Earth
From the expression g = GM/R2, the mass of the Earth can be calculated as follows :

M = gR2/G = 9.8x(6.38×106)2/6.67×10^−11 = 5.98 × 102^4 kg