Angular motion
When a rigid body rotates about a fixed axis all points on the body are constrained to move in a circular path. Therefore in any given period of time all points on the body will complete the same number of revolutions about the axis of rotation; that is, the speed of rotation is referred to in terms of revolutions per minute (rev/min). However, for many engineering problems it is often necessary to express the speed of rotation in terms of the angle in radians turned through in unit time.

 The radian
A radian is the angle subtended at the centre of a circle by an arc equal in length to the radius of that circle. This is shown in Fig. 1(a). The relationship between arc length, radius and angle in radians is shown in Fig. 1(b).

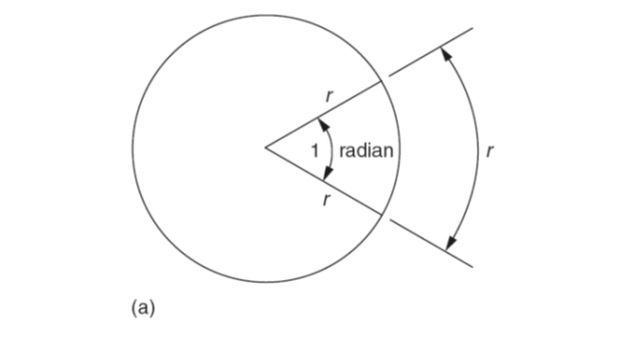
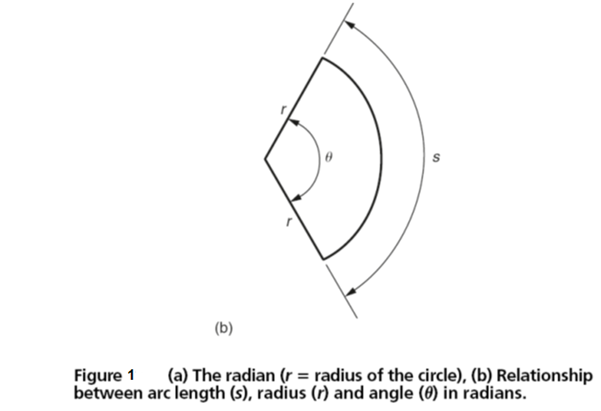
Where:

s = length of arc

θ = angle in radians

r = radius of the circle

From the definition of a radian:

s/r = θ therefore s = rθ

In the expression s = rθ if s is equal to the circumference of a circle then:

2πr = rθ therefore 2π =θ

That is, 1 revolution = 2π radians (=360°)

Similarly 1 radian = 360/2π = 57.3° (approximately).

Angular displacement
In linear motion the symbol s represents the distance travelled in a straight line; that is, the linear displacement. In angular motion, the Greek letter θ is the corresponding symbol for the displacement measured in radians.

 Angular velocity
A rigid body rotating about a fixed axis O at a uniform speed of n rev/s turns through 2 π radians (rad) in each revolution. Therefore the angular velocity ω (Greek letter omega) is given by the expression:

ω =2 π n rad/s

Further, if the body rotates through an angle of θ radians in time t seconds then, if that motion is uniform,

The angular velocity ω =θ/t rad/s

Note that angular velocity has no linear dimensions.

The relationship between angular and linear velocity
Consider the point A on the outer rim of the solid body shown in Fig. 2. If the body rotates through θ (rad) in t (seconds), and using length of arc = angle in radians × radius

s = rθ

then to obtain the average velocity divide both sides of the expression by t so that:

s/t =r(θ/t)

but

s/t = v and θ/t = ω

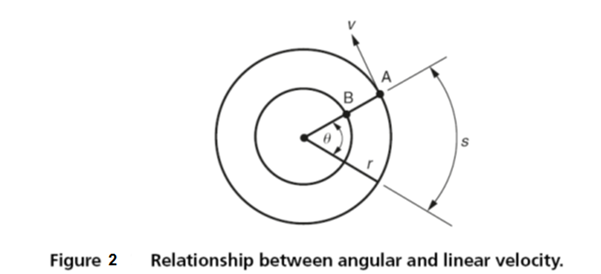
Therefore:

v = r ω or linear velocity = angular velocity × radius.

Note:

1. The point B on the body has the same angular velocity as A but has a smaller linear velocity since it has a smaller radius.
2. If the radius r is in metres and the angular velocity ω is expressed in rad/s, then the linear velocity v is expressed in m/s. Sometimes the angular velocity is expressed in rev/min. It is necessary to convert rev/min to rad/s before substituting in expressions such as v = r ω:

N (rev/min) = 2 π N (rad/min) = 2 π N/60 (rad/s)

Angular acceleration
A similar relationship to that of linear and angular velocity exist between linear and angular acceleration. That is:

a = r α

where:

a = linear acceleration, r = radius, α (Greek letter alpha) = angular acceleration.

Similarly there is a set of expression for the relationships between angular velocity and acceleration. These are:

ω ₂ = ω ₁ + α t          ω ₁ = initial angular velocity

θ=[( ω ₁ + ω ₂)/2] × t     ω ₂ = final angular velocity

θ = ω ₁t  + 1⁄2 α t ²     α = angular acceleration

ω ₂ ² = ω ₁ ² + 2 α θ      θ= angle of rotation

θ= ω ₂t  – 1⁄2 α t²         t = time taken