Centripetal acceleration and centripetal force
The dictionary definition of centripetal acceleration states that it is the acceleration directed towards the centre of curvature of the path of a body which is moving along that path with constant speed. Its value is v²/r where v is the speed and r is the radius of curvature or its value can be expressed as ω ²r where ω is the angular velocity.

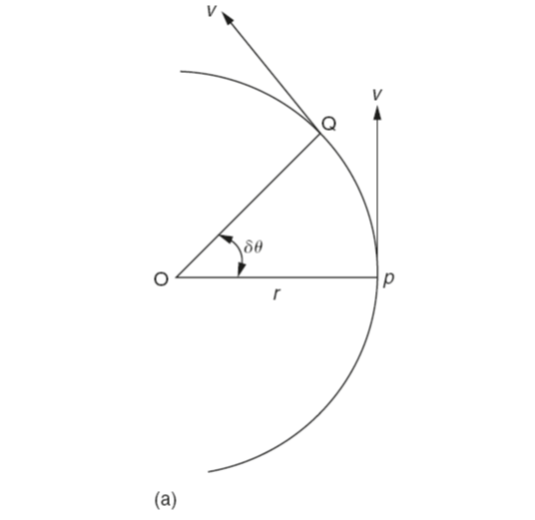
Figure 1(a) shows a body of mass m moving along a circular path of radius r and centre O with a constant angular velocity ω. When the body is a point P it possesses an instantaneous linear velocity v tangential to the circumference of the circle along which it is travelling.

During an incremental period of time, δ t, the body moves along the circumference of the circle from P to Q. The angle subtended by this translation from P to Q is δθ. Although the body is moving at constant speed, it is not moving along the same line of action. Therefore, there is a change in the velocity of the body. Since there is a change of velocity with respect to time the body is, by definition, subjected to an acceleration.

Figure 1(b) shows the velocity vector diagram where:

• Vector Op represents the velocity (speed and direction) at point P.
• Vector Oq represents the velocity at point Q.
• Vector pq represents the radial change in velocity during the translation of the body from P to Q.

The radial change in velocity = pq = v ×  δθ

However:
θ= ω t

Therefore:
δθ= ω × δt = (v/r) × δt

Thus:
The vector change in velocity = (v² × δt)/(r × δt) = v²/r = ω ²r

In this discussion the centripetal acceleration refers to a body of mass m. From Newton’s second law of motion a body cannot be accelerated unless an external force acts on that body. Therefore the centripetal force producing the acceleration = mass × acceleration.

Expressed mathematically:
Centripetal force = m × (v²/r) = m ω ²r

 Centrifugal force
Newton’s third law states that: for every acting force there is an equal and opposite reaction force. Therefore there must be an opposing reaction force equal and opposite to the centripetal force. This opposing force acts radially outwards and is known as the centrifugal force. Consider a railway train going round a curve. The train wheel flanges push outwards on the rails (centrifugal force) whilst the rails exert a force of equal magnitude on the wheels of the train pushing inwards (centripetal force). Similarly, when a mass restrained by a cord is whirled about an axis, the centrifugal force tries to pull the mass outwards whilst the centripetal force tries to pull the mass inwards, thus the cord is kept in tension.