The basic knowledge of various kinds of forces and motion is highly desirable for engineering and practical applications. The Newton’s laws of motion defines and gives the expression for the force. Force is a vector quantity and can be combined according to the rules of vector algebra. A force can be graphically represented by a straight line with an arrow, in which the length of the line is proportional to the magnitude of the force and the arrowhead indicates its direction.

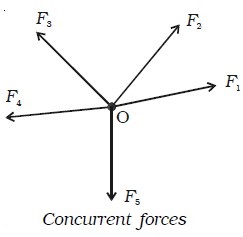
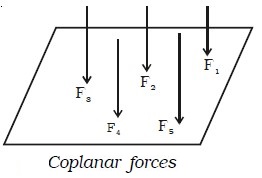
A force system is said to be concurrent, if the lines of all forces intersect at a common point (Fig above). A force system is said to be coplanar, if the lines of the action of all forces lie in one plane (Fig below).

Resultant of a system of forces acting on a rigid body
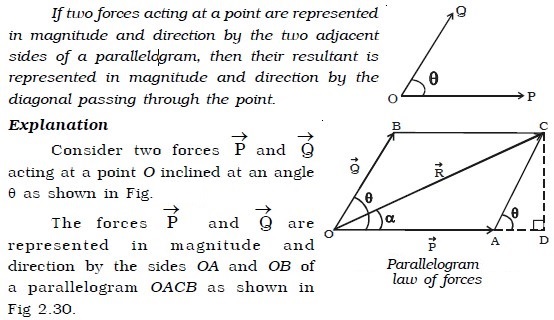
If two or more forces act simultaneously on a rigid body, it is possible to replace the forces by a single force, which will produce the same effect on the rigid body as the effect produced jointly by several forces. This single force is the resultant of the system of forces. If →P and →Q are two forces acting on a body simultaneously in the same direction, their resultant is →R = → P + →Q and it acts in the same direction as that of the forces. If →P and →Q act in opposite directions, their resultant →R is → R = →P ~ →Q and the resultant is in the direction of the greater force. If the forces →P and → Q act in directions which are inclined to each other, their resultant can be found by using parallelogram law of forces and triangle law of forces.

Parallelogram law of forces

Triangle law of forces
The resultant of two forces acting at a point can also be found by using triangle law of forces. If two forces acting at a point are represented in magnitude and direction by the two adjacent sides of a triangle taken in order, then the closing side of the triangle taken in the reversed order represents the resultant of the forces in magnitude and direction.

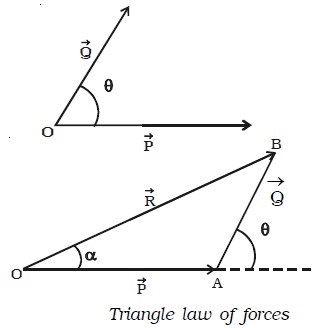
Forces →P and →Q act at an angle θ. In order to find the resultant of →P and → Q, one can apply the head to tail method, to construct the triangle. In Fig. above, OA and AB represent →P and → Q in magnitude and direction. The closing side OB of the triangle taken in the reversed order represents the resultant →R of the forces →P and → Q. The magnitude and the direction of → R can be found by using sine and cosine laws of triangles. The triangle law of forces can also be stated as, if a body is in equilibrium under the action of three forces acting at a point, then the three forces can be completely represented by the three sides of a triangle taken in order. If →P , →Q and →R are the three forces acting at a point and they are represented by the three sides of a triangle then P/OA = Q/AB = R/OB

Equilibrant
According to Newton’s second law of motion, a body moves with a velocity if it is acted upon by a force. When the body is subjected to number of concurrent forces, it moves in a direction of the resultant force. However, if another force, which is equal in magnitude of the resultant but opposite in direction, is applied to a body, the body comes to rest. Hence, equilibrant of a system of forces is a single force, which acts along with the other forces to keep the body in equilibrium. Let us consider the forces F1. F2, F3 and F4 acting on a body O as shown in Fig. below a. If F is the resultant of all the forces and in order to keep the body at rest, an equal force (known as equilibrant) should act on it in the opposite direction as shown in Fig. below b.

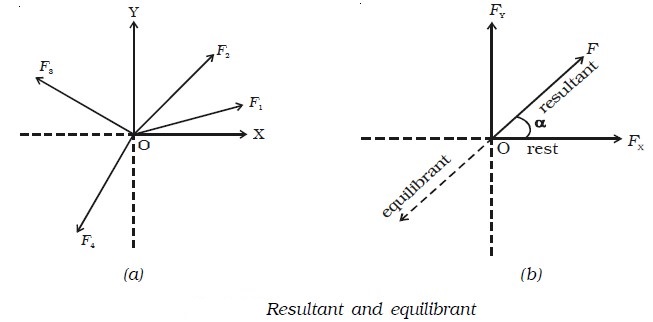
From Fig. above b, it is found that, resultant = − equilibrant

Resultant of concurrent forces
Consider a body O, which is acted upon by four forces as shown in Fig. below a. Let θ1, θ2, θ3 and θ4 be the angles made by the forces with respect to X-axis. Each force acting at O can be replaced by its rectangular components F1x and F1y, F2x and F2y, .. etc., For example, for the force →F 1 making an angle θ1, its components are, F1x =F1 cos θ1 and F1y= F1 sin θ1. These components of forces produce the same effect on the body as the forces themselves. The algebraic sum of the horizontal components

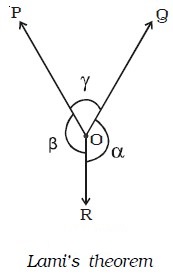
Lami’s theorem
It gives the conditions of equilibrium for three forces acting at a point. Lami’s theorem states that if three forces acting at a point are in equilibrium, then each of the force is directly proportional to the sine of the angle between the remaining two forces. Let us consider three forces →P , →Q and → R acting at a point O (Fig below). Under the action of three forces, the point O is at rest, then by Lami’s theorem,
P ∝ sin α
Q ∝ sin β
and R ∝ sin γ, then
P/sin∝ = Q/sinβ = R/sinγ = constant

Experimental verification of triangle law, parallelogram law and Lami’s theorem
Two smooth small pulleys are fixed, one each at the top corners of a drawing board kept vertically on a wall as shown in Fig. below. The pulleys should move freely without any friction. A light string is made to pass over both the pulleys. Two slotted weights P and Q (of the order of 50 g) are taken and are tied to the two free ends of the string. Another short string is tied to the centre of the first string at O. A third slotted weight R is attached to the free end of the short string. The weights P, Q and R are adjusted such that the system is at rest.

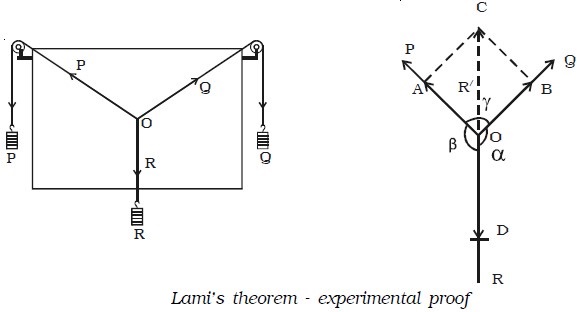
The point O is in equilibrium under the action of the three forces P, Q and R acting along the strings. Now, a sheet of white paper is held just behind the string without touching them. The common knot O and the directions of OA, OB and OD are marked to represent in magnitude, the three forces P, Q and R on any convenient scale (like 50 g = 1 cm). The experiment is repeated for different values of P, Q and R and the values are tabulated.

To verify parallelogram law
To determine the resultant of two forces P and Q, a parallelogram OACB is completed, taking OA representing P, OB representing Q and the diagonal OC gives the resultant. The length of the diagonal OC and the angle COD are measured and tabulated (Table below).

OC is the resultant R′ of P and Q. Since O is at rest, this resultant R′ must be equal to the third force R (equilibrant) which acts in the opposite direction. OC = OD. Also, both OC and OD are acting in the opposite direction. ∠COD must be equal to 180°. If OC = OD and ∠COD = 180°, one can say that parallelogram law of force is verified experimentally.

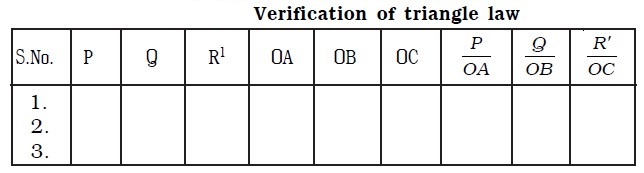
To verify Triangle Law
According to triangle law of forces, the resultant of P (= OA = BC) and Q (OB) is represented in magnitude and direction by OC which is taken in the reverse direction. Alternatively, to verify the triangle law of forces, the ratios , P Q OA OB and R OC ′ are calculated and are tabulated (Table below). It will be found out that, all the three ratios are equal, which proves the triangle law of forces experimentally.

To verify Lami’s theorem
To verify Lami’s theorem, the angles between the three forces, P, Q and R (i.e) ∠BOD = α, ∠AOD = β and ∠AOB = γ are measured using protractor and tabulated (Table below). The ratios sin Pα , sinQβ and sinRγ are calculated and it is found that all the three ratios are equal and this verifies the Lami’s theorem.

Conditions of equilibrium of a rigid body acted upon by a system of concurrent forces in plane
● If an object is in equilibrium under the action of three forces, the resultant of two forces must be equal and opposite to the third force. Thus, the line of action of the third force must pass through the point of intersection of the lines of action of the other two forces. In other words, the system of three coplanar forces in equilibrium, must obey parallelogram law, triangle law of forces and Lami’s theorem. This condition ensures the absence of translational motion in the system.
● The algebraic sum of the moments about any point must be equal to zero. Σ M = 0 (i.e) the sum of clockwise moments about any point must be equal to the sum of anticlockwise moments about the same point. This condition ensures, the absence of rotational motion.