Converting Units
To convert a quantity in terms of one unit to an equivalent in new units, multiply by a “conversion factor” — a ratio of equivalent quantities.
Conversion factors are dimensionless (but not unit-less) and numerically equivalent to unity.
![]()
Both the numerator of the conversion factor (2.54 cm) and its denominator (1 in) have dimensions of length, so the ratio is dimensionless. Both also describe the same “magnitude” of length, so the ratio is equivalent to one and can multiply both sides of an equation without changing its nature.
When you apply a conversion factor, the old units cancel out and the new units remain.
![]()
This is the preferred way for engineers to do unit conversions because it makes it clear what has been done and makes the work easy to check and understand. Don’t worry about finding a single factor to do the conversion at one swoop; it is perfectly normal to string several along in a row.
EXAMPLE: Convert 5 m.p.h. to yds/week
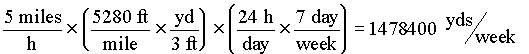
You want to do your conversions efficiently — and spend only the necessary time looking up values. Often it is faster to use several conversion factors that you already know, rather than spend time looking up a single factor that will do the change all at once.
EXAMPLE: What is the conversion factor between Btu/h and W?
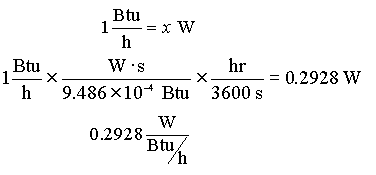
Carrying units through a calculation can be helpful in figuring out a problem. Often, looking at the units provides a clue as to what step needs to be taken next. It also helps prevent silly mistakes, such as accidentally multiplying when you mean to divide.
EXAMPLE: Felder & Rousseau (1978), prblm 2-5
It is 1953 and your Mercury has been giving you 17 miles to the gallon. The average cost of gasoline between Baton Rouge and Bogalusa, a distance of about 100 miles, is 55 cents a gallon. How much does it cost to make the trip?
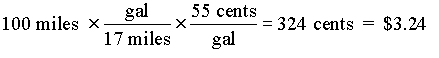
I want to point out two mistakes beginners often make when applying conversion factors. First, people will sometimes write out the factor with the numbers upside down. This is usually because they misinterpret the arrangement of the conversion factor table. To avoid this mistake, try to think about the relative size of the units when you write down a factor (i.e. inches are smaller than feet, so the number on the inches side of the line should be bigger).
The other common error has to do with units that are raised to powers, such as “square feet” or “cubic meters”. The conversion factors for these need to be raised to the same power as the unit; to go from cubic meters to cubic feet, you use the conversion from meter to foot, but raise everything (numbers and units) to the 3rd power.
![]()
I’ve graded a lot of papers where people didn’t apply the power to the number — so watch this one.
“Dimensional” Equations
Often, books that are trying to be “practical” present equations and formulae that are unit specific, instead of using more “theoretical” forms that work with any set of units. Handbooks for practicing engineers of such dimensional equations.
For instance, if we want to calculate the power needed for a fan to move a volume rate of air through a pressure difference, the general formula is:
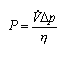
This formula can be used for any type of units. For instance, let us put in pressure in Pa, flow in ft3/hour, and get an answer in Watts.
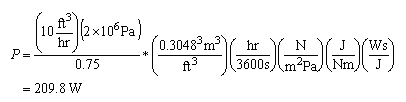
But what if we know that we are going to do this same calculation over and over again? It might make sense to develop a special form of the equation just for our use.
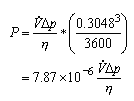
Now the units of the formula are “built-in”. A user can be told “if you plug in quantity A in these units, and quantity B in those units, the answer will be in thise units”.
These kinds of dimensional formulas are encountered in many cases. They are convenient when calculations have become standardized and repetitious; however, they can be tricky unless you are careful. They must be used with the units provided. If you look back over how we came up with the equation, you’ll note that the numerical constant in the formula has units attached — even though they aren’t written out.
When you come across a formula in a book and units for the variables are specified, you need to be aware that the constants may also have units traveling incognito. For instance, the formula for liquid flow through a pipe can be (very roughly) approximated by:
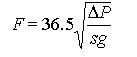
where F is in gal/min, Delta P is the pressure difference in psi between the entrance and exit of the pipe, and sg is the specific gravity of the flowing fluid. If the answer comes out in gpm, but we didn’t put gallons in anywhere, there have to be some unit conversions hidden in the equation.
If you want to use the equation in any way except with the exact given units, you need to examine the equation to determine the hidden units. This isn’t hard, but for some of you may take a little practice. For the flow equation, they come out to be
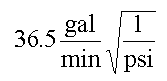
Being able to “back out” the units of an equation is a useful skill, and one that helps with a variety of engineering and thermodynamics problems. It might be a useful exercise to spend some time practicing looking at an equation and thinking of it in terms of units only.
Transforming a Dimensional Equation
Now suppose that you want to use the flow equation with different units, say m3/second and Pascals. If you only have to do it one time, it isn’t hard to convert Pascals to psi, plug the psi into the equation to get gpm, and then convert the gpm to m3/s. But you may be doing an experiment or problem where you need to use the dimensional equation repeatedly. In this case, it makes sense to transform the dimensional equation to the new set of units.
This isn’t very difficult. Just remember that the constant (36.5) has all the units attached that make the equation work. All you have to do is convert those attached units:
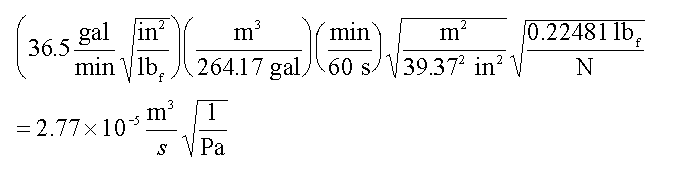
and you have a perfectly good new equation (let’s throw “primes” on F and Delta P to indicate the changed units
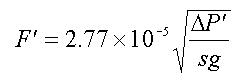
The problem is made easier because specific gravity is a ratio of two densities, and so for this use, can be treated as dimensionless.
Converting Units
To convert a quantity in terms of one unit to an equivalent in new units, multiply by a “conversion factor” — a ratio of equivalent quantities.
Conversion factors are dimensionless (but not unit-less) and numerically equivalent to unity.
![]()
Both the numerator of the conversion factor (2.54 cm) and its denominator (1 in) have dimensions of length, so the ratio is dimensionless. Both also describe the same “magnitude” of length, so the ratio is equivalent to one and can multiply both sides of an equation without changing its nature.
When you apply a conversion factor, the old units cancel out and the new units remain.
![]()
This is the preferred way for engineers to do unit conversions because it makes it clear what has been done and makes the work easy to check and understand. Don’t worry about finding a single factor to do the conversion at one swoop; it is perfectly normal to string several along in a row.
EXAMPLE: Convert 5 m.p.h. to yds/week
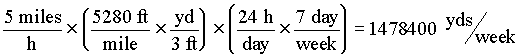
You want to do your conversions efficiently — and spend only the necessary time looking up values. Often it is faster to use several conversion factors that you already know, rather than spend time looking up a single factor that will do the change all at once.
EXAMPLE: What is the conversion factor between Btu/h and W?
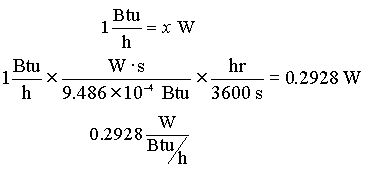
Carrying units through a calculation can be helpful in figuring out a problem. Often, looking at the units provides a clue as to what step needs to be taken next. It also helps prevent silly mistakes, such as accidentally multiplying when you mean to divide.
EXAMPLE: Felder & Rousseau (1978), prblm 2-5
It is 1953 and your Mercury has been giving you 17 miles to the gallon. The average cost of gasoline between Baton Rouge and Bogalusa, a distance of about 100 miles, is 55 cents a gallon. How much does it cost to make the trip?
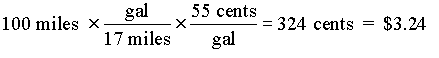
I want to point out two mistakes beginners often make when applying conversion factors. First, people will sometimes write out the factor with the numbers upside down. This is usually because they misinterpret the arrangement of the conversion factor table. To avoid this mistake, try to think about the relative size of the units when you write down a factor (i.e. inches are smaller than feet, so the number on the inches side of the line should be bigger).
The other common error has to do with units that are raised to powers, such as “square feet” or “cubic meters”. The conversion factors for these need to be raised to the same power as the unit; to go from cubic meters to cubic feet, you use the conversion from meter to foot, but raise everything (numbers and units) to the 3rd power.
![]()
I’ve graded a lot of papers where people didn’t apply the power to the number — so watch this one.
“Dimensional” Equations
Often, books that are trying to be “practical” present equations and formulae that are unit specific, instead of using more “theoretical” forms that work with any set of units. Handbooks for practicing engineers of such dimensional equations.
For instance, if we want to calculate the power needed for a fan to move a volume rate of air through a pressure difference, the general formula is:
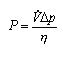
This formula can be used for any type of units. For instance, let us put in pressure in Pa, flow in ft3/hour, and get an answer in Watts.
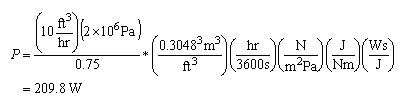
But what if we know that we are going to do this same calculation over and over again? It might make sense to develop a special form of the equation just for our use.
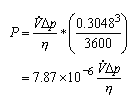
Now the units of the formula are “built-in”. A user can be told “if you plug in quantity A in these units, and quantity B in those units, the answer will be in thise units”.
These kinds of dimensional formulas are encountered in many cases. They are convenient when calculations have become standardized and repetitious; however, they can be tricky unless you are careful. They must be used with the units provided. If you look back over how we came up with the equation, you’ll note that the numerical constant in the formula has units attached — even though they aren’t written out.
When you come across a formula in a book and units for the variables are specified, you need to be aware that the constants may also have units traveling incognito. For instance, the formula for liquid flow through a pipe can be (very roughly) approximated by:

where F is in gal/min, Delta P is the pressure difference in psi between the entrance and exit of the pipe, and sg is the specific gravity of the flowing fluid. If the answer comes out in gpm, but we didn’t put gallons in anywhere, there have to be some unit conversions hidden in the equation.
If you want to use the equation in any way except with the exact given units, you need to examine the equation to determine the hidden units. This isn’t hard, but for some of you may take a little practice. For the flow equation, they come out to be
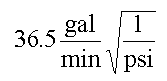
Being able to “back out” the units of an equation is a useful skill, and one that helps with a variety of engineering and thermodynamics problems. It might be a useful exercise to spend some time practicing looking at an equation and thinking of it in terms of units only.
Transforming a Dimensional Equation
Now suppose that you want to use the flow equation with different units, say m3/second and Pascals. If you only have to do it one time, it isn’t hard to convert Pascals to psi, plug the psi into the equation to get gpm, and then convert the gpm to m3/s. But you may be doing an experiment or problem where you need to use the dimensional equation repeatedly. In this case, it makes sense to transform the dimensional equation to the new set of units.
This isn’t very difficult. Just remember that the constant (36.5) has all the units attached that make the equation work. All you have to do is convert those attached units:
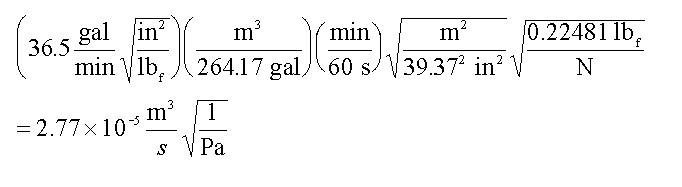
and you have a perfectly good new equation (let’s throw “primes” on F and Delta P to indicate the changed units
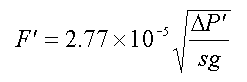
The problem is made easier because specific gravity is a ratio of two densities, and so for this use, can be treated as dimensionless.
Converting Units
To convert a quantity in terms of one unit to an equivalent in new units, multiply by a “conversion factor” — a ratio of equivalent quantities.
Conversion factors are dimensionless (but not unit-less) and numerically equivalent to unity.
![]()
Both the numerator of the conversion factor (2.54 cm) and its denominator (1 in) have dimensions of length, so the ratio is dimensionless. Both also describe the same “magnitude” of length, so the ratio is equivalent to one and can multiply both sides of an equation without changing its nature.
When you apply a conversion factor, the old units cancel out and the new units remain.
![]()
This is the preferred way for engineers to do unit conversions because it makes it clear what has been done and makes the work easy to check and understand. Don’t worry about finding a single factor to do the conversion at one swoop; it is perfectly normal to string several along in a row.
EXAMPLE: Convert 5 m.p.h. to yds/week
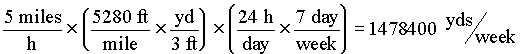
You want to do your conversions efficiently — and spend only the necessary time looking up values. Often it is faster to use several conversion factors that you already know, rather than spend time looking up a single factor that will do the change all at once.
EXAMPLE: What is the conversion factor between Btu/h and W?

Carrying units through a calculation can be helpful in figuring out a problem. Often, looking at the units provides a clue as to what step needs to be taken next. It also helps prevent silly mistakes, such as accidentally multiplying when you mean to divide.
EXAMPLE: Felder & Rousseau (1978), prblm 2-5
It is 1953 and your Mercury has been giving you 17 miles to the gallon. The average cost of gasoline between Baton Rouge and Bogalusa, a distance of about 100 miles, is 55 cents a gallon. How much does it cost to make the trip?
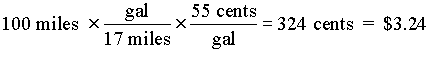
I want to point out two mistakes beginners often make when applying conversion factors. First, people will sometimes write out the factor with the numbers upside down. This is usually because they misinterpret the arrangement of the conversion factor table. To avoid this mistake, try to think about the relative size of the units when you write down a factor (i.e. inches are smaller than feet, so the number on the inches side of the line should be bigger).
The other common error has to do with units that are raised to powers, such as “square feet” or “cubic meters”. The conversion factors for these need to be raised to the same power as the unit; to go from cubic meters to cubic feet, you use the conversion from meter to foot, but raise everything (numbers and units) to the 3rd power.
![]()
I’ve graded a lot of papers where people didn’t apply the power to the number — so watch this one.
“Dimensional” Equations
Often, books that are trying to be “practical” present equations and formulae that are unit specific, instead of using more “theoretical” forms that work with any set of units. Handbooks for practicing engineers of such dimensional equations.
For instance, if we want to calculate the power needed for a fan to move a volume rate of air through a pressure difference, the general formula is:
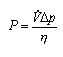
This formula can be used for any type of units. For instance, let us put in pressure in Pa, flow in ft3/hour, and get an answer in Watts.

But what if we know that we are going to do this same calculation over and over again? It might make sense to develop a special form of the equation just for our use.
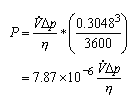
Now the units of the formula are “built-in”. A user can be told “if you plug in quantity A in these units, and quantity B in those units, the answer will be in thise units”.
These kinds of dimensional formulas are encountered in many cases. They are convenient when calculations have become standardized and repetitious; however, they can be tricky unless you are careful. They must be used with the units provided. If you look back over how we came up with the equation, you’ll note that the numerical constant in the formula has units attached — even though they aren’t written out.
When you come across a formula in a book and units for the variables are specified, you need to be aware that the constants may also have units traveling incognito. For instance, the formula for liquid flow through a pipe can be (very roughly) approximated by:

where F is in gal/min, Delta P is the pressure difference in psi between the entrance and exit of the pipe, and sg is the specific gravity of the flowing fluid. If the answer comes out in gpm, but we didn’t put gallons in anywhere, there have to be some unit conversions hidden in the equation.
If you want to use the equation in any way except with the exact given units, you need to examine the equation to determine the hidden units. This isn’t hard, but for some of you may take a little practice. For the flow equation, they come out to be
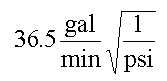
Being able to “back out” the units of an equation is a useful skill, and one that helps with a variety of engineering and thermodynamics problems. It might be a useful exercise to spend some time practicing looking at an equation and thinking of it in terms of units only.
Transforming a Dimensional Equation
Now suppose that you want to use the flow equation with different units, say m3/second and Pascals. If you only have to do it one time, it isn’t hard to convert Pascals to psi, plug the psi into the equation to get gpm, and then convert the gpm to m3/s. But you may be doing an experiment or problem where you need to use the dimensional equation repeatedly. In this case, it makes sense to transform the dimensional equation to the new set of units.
This isn’t very difficult. Just remember that the constant (36.5) has all the units attached that make the equation work. All you have to do is convert those attached units:
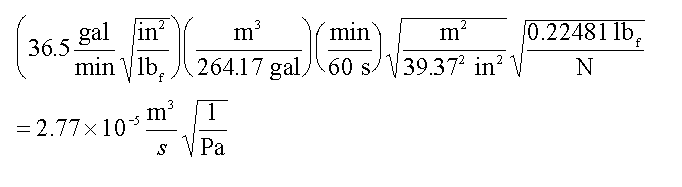
and you have a perfectly good new equation (let’s throw “primes” on F and Delta P to indicate the changed units
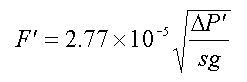
The problem is made easier because specific gravity is a ratio of two densities, and so for this use, can be treated as dimensionless.
Converting Units
To convert a quantity in terms of one unit to an equivalent in new units, multiply by a “conversion factor” — a ratio of equivalent quantities.
Conversion factors are dimensionless (but not unit-less) and numerically equivalent to unity.
![]()
Both the numerator of the conversion factor (2.54 cm) and its denominator (1 in) have dimensions of length, so the ratio is dimensionless. Both also describe the same “magnitude” of length, so the ratio is equivalent to one and can multiply both sides of an equation without changing its nature.
When you apply a conversion factor, the old units cancel out and the new units remain.
![]()
This is the preferred way for engineers to do unit conversions because it makes it clear what has been done and makes the work easy to check and understand. Don’t worry about finding a single factor to do the conversion at one swoop; it is perfectly normal to string several along in a row.
EXAMPLE: Convert 5 m.p.h. to yds/week
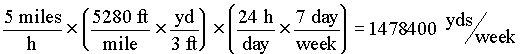
You want to do your conversions efficiently — and spend only the necessary time looking up values. Often it is faster to use several conversion factors that you already know, rather than spend time looking up a single factor that will do the change all at once.
EXAMPLE: What is the conversion factor between Btu/h and W?
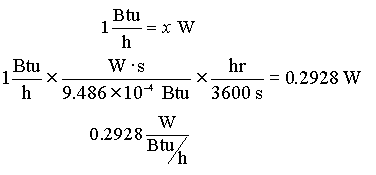
Carrying units through a calculation can be helpful in figuring out a problem. Often, looking at the units provides a clue as to what step needs to be taken next. It also helps prevent silly mistakes, such as accidentally multiplying when you mean to divide.
EXAMPLE: Felder & Rousseau (1978), prblm 2-5
It is 1953 and your Mercury has been giving you 17 miles to the gallon. The average cost of gasoline between Baton Rouge and Bogalusa, a distance of about 100 miles, is 55 cents a gallon. How much does it cost to make the trip?
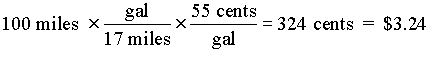
I want to point out two mistakes beginners often make when applying conversion factors. First, people will sometimes write out the factor with the numbers upside down. This is usually because they misinterpret the arrangement of the conversion factor table. To avoid this mistake, try to think about the relative size of the units when you write down a factor (i.e. inches are smaller than feet, so the number on the inches side of the line should be bigger).
The other common error has to do with units that are raised to powers, such as “square feet” or “cubic meters”. The conversion factors for these need to be raised to the same power as the unit; to go from cubic meters to cubic feet, you use the conversion from meter to foot, but raise everything (numbers and units) to the 3rd power.
![]()
I’ve graded a lot of papers where people didn’t apply the power to the number — so watch this one.
“Dimensional” Equations
Often, books that are trying to be “practical” present equations and formulae that are unit specific, instead of using more “theoretical” forms that work with any set of units. Handbooks for practicing engineers of such dimensional equations.
For instance, if we want to calculate the power needed for a fan to move a volume rate of air through a pressure difference, the general formula is:
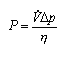
This formula can be used for any type of units. For instance, let us put in pressure in Pa, flow in ft3/hour, and get an answer in Watts.
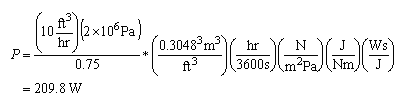
But what if we know that we are going to do this same calculation over and over again? It might make sense to develop a special form of the equation just for our use.
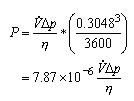
Now the units of the formula are “built-in”. A user can be told “if you plug in quantity A in these units, and quantity B in those units, the answer will be in thise units”.
These kinds of dimensional formulas are encountered in many cases. They are convenient when calculations have become standardized and repetitious; however, they can be tricky unless you are careful. They must be used with the units provided. If you look back over how we came up with the equation, you’ll note that the numerical constant in the formula has units attached — even though they aren’t written out.
When you come across a formula in a book and units for the variables are specified, you need to be aware that the constants may also have units traveling incognito. For instance, the formula for liquid flow through a pipe can be (very roughly) approximated by:
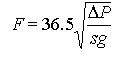
where F is in gal/min, Delta P is the pressure difference in psi between the entrance and exit of the pipe, and sg is the specific gravity of the flowing fluid. If the answer comes out in gpm, but we didn’t put gallons in anywhere, there have to be some unit conversions hidden in the equation.
If you want to use the equation in any way except with the exact given units, you need to examine the equation to determine the hidden units. This isn’t hard, but for some of you may take a little practice. For the flow equation, they come out to be
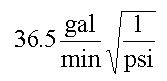
Being able to “back out” the units of an equation is a useful skill, and one that helps with a variety of engineering and thermodynamics problems. It might be a useful exercise to spend some time practicing looking at an equation and thinking of it in terms of units only.
Transforming a Dimensional Equation
Now suppose that you want to use the flow equation with different units, say m3/second and Pascals. If you only have to do it one time, it isn’t hard to convert Pascals to psi, plug the psi into the equation to get gpm, and then convert the gpm to m3/s. But you may be doing an experiment or problem where you need to use the dimensional equation repeatedly. In this case, it makes sense to transform the dimensional equation to the new set of units.
This isn’t very difficult. Just remember that the constant (36.5) has all the units attached that make the equation work. All you have to do is convert those attached units:

and you have a perfectly good new equation (let’s throw “primes” on F and Delta P to indicate the changed units
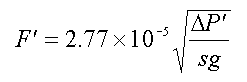
The problem is made easier because specific gravity is a ratio of two densities, and so for this use, can be treated as dimensionless.

