There are many examples in practice where two forces, acting together, exert a moment, or turning effect on some object. As a very simple case, suppose two strings are tied to a wheel at the points X and Y, and two equal and opposite forces, F, are exerted tangentially to the wheels (Fig. below). If the wheel is pivoted at its centre O it begins to rotate about O in an anticlockwise direction. Two equal and opposite forces whose lines of action do not coincide are said to constitute a couple in mechanics. The two forces always have a turning effect, or moment, called a torque. The perpendicular distance between the lines of action of two forces, which constitute the couple, is called the arm of the couple.

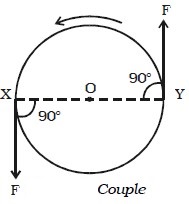
The product of the forces forming the couple and the arm of the couple is called the moment of the couple or torque.
Torque = one of the forces × perpendicular distance between the forces
The torque in rotational motion plays the same role as the force in translational motion. A quantity that is a measure of this rotational effect produced by the force is called torque.
In vector notation, →τ = →r × →F
The torque is maximum when θ = 90° (i.e) when the applied force is at right angles to →r.
Examples of couple are
● Forces applied to the handle of a screw press,
● Opening or closing a water tap.
● Turning the cap of a pen.
● Steering a car.

Work done by a couple
Suppose two equal and opposite forces F act tangentially to a wheel W, and rotate it through an angle θ (Fig. below).

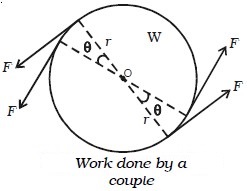
Then the work done by each force = Force × distance = F × r θ
(since r θ is the distance moved by a point on the rim)
Total work done W = F r θ + F r θ = 2F r θ
but torque τ = F × 2r = 2F r
∴ work done by the couple, W = τ θ