Dimensions of a physical quantity are the powers to which the fundamental quantities must be raised.

We know that velocity = displacement / time
= [L ] / [T ]
= [MoL1T−1]
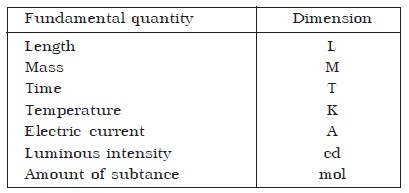
where [M], [L] and [T] are the dimensions of the fundamental quantities mass, length and time respectively.

Therefore velocity has zero dimension in mass, one dimension in length and −1 dimension in time. Thus the dimensional formula for
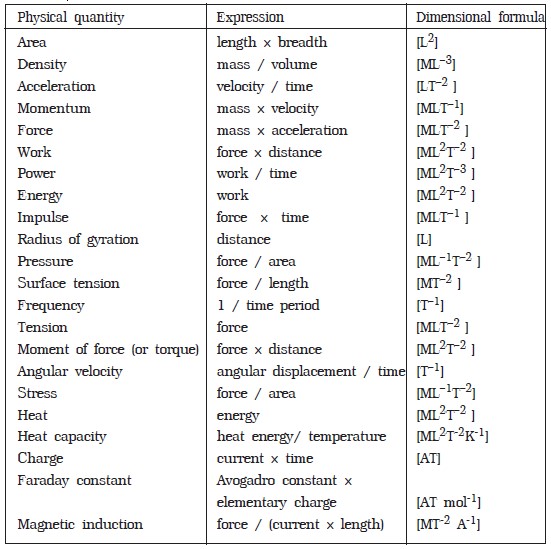
velocity is [MoL1T−1] or simply [LT−1].The dimensions of fundamental quantities are given in Table 1.4 and the dimensions of some derived quantities are given in Table 1.5

Dimensions of fundamental quantities

Dimensional formulae of some derived quantities

Dimensional quantities
Constants which possess dimensions are called dimensional constants. Planck’s constant, universal gravitational constant are dimensional constants. Dimensional variables are those physical quantities which possess dimensions but do not have a fixed value. Example − velocity, force, etc.

Dimensionless quantities
There are certain quantities which do not possess dimensions. They are called dimensionless quantities. Examples are strain, angle,
specific gravity, etc. They are dimensionless as they are the ratio of two quantities having the same dimensional formula.

Principle of homogeneity of dimensions
An equation is dimensionally correct if the dimensions of the various terms on either side of the equation are the same. This is called the principle of homogeneity of dimensions. This principle is based on the fact that two quantities of the same dimension only can be added up, the resulting quantity also possessing the same dimension. The equation A + B = C is valid only if the dimensions of A, B and C are the same.

Uses of dimensional analysis
The method of dimensional analysis is used to
● convert a physical quantity from one system of units to another.
● check the dimensional correctness of a given equation.
● establish a relationship between different physical quantities in an equation.

To convert a physical quantity from one system of units to another
Given the value of G in cgs system is 6.67 × 10−8dyne cm2 g−2.
Calculate its value in SI units.

The dimensional formula for gravitational constant is [M−1L3T −2].
In cgs system, dimensional formula for G is [M1x L1y T1z].
In SI system, dimensional formula for G is [M2x L2x T2x]
Here x = −1, y = 3, z = −2

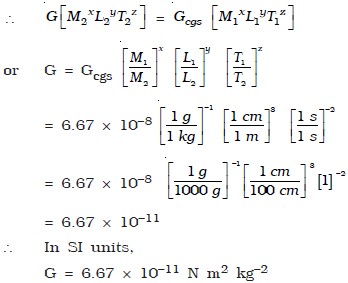
To check the dimensional correctness of a given equation
Let us take the equation of motion
s = ut + (½)at2
Applying dimensions on both sides
[L] = [LT−1] [T] + [LT−2] [T2]
(½ is a constant having no dimension)
[L] = [L] + [L]
As the dimensions on both sides are the same, the equation is dimensionally correct.

To establish a relationship between the physical quantities in an equation
Let us find an expression for the time period T of a simple pendulum. The time period T may depend upon (i) mass m of the bob (ii) length l of the pendulum and (iii) acceleration due to gravity g at the place where the pendulum is suspended.
(i.e) T α mx ly gz
or T = k mx ly gz
where k is a dimensionless constant of propotionality. Rewriting equation (1) with dimensions
[T1] = [Mx] [L y] [LT−2]z
[T1] = [Mx L y + z T−2z]
Comparing the powers of M, L and T on both sides
x = 0, y + z = 0 and −2z = 1
Solving for x, y and z, x = 0, y = ½ and z = –½
From equation (1), T = k mo l½ g−½
T = k[l/g]1/2 = k √l/g
Experimentally the value of k is determined to be 2π.
∴ T = 2π √l/g

Limitations of Dimensional Analysis
● The value of dimensionless constants cannot be determined by this method.
● This method cannot be applied to equations involving exponential and trigonometric functions.
● It cannot be applied to an equation involving more than three physical quantities.
● It can check only whether a physical relation is dimensionally correct or not. It cannot tell whether the relation is absolutely correct or not. For example applying this technique s = ut + 1/4 at2 is dimensionally correct whereas the correct relation is s = ut + 1/2 at2.