Consider a small cylinder of fluid PQ as illustrated in Fig.(1)  [2]. If the fluid is at rest, the cylinder  must be in equilibrium  and  the only forces acting  on it are those on its various faces (due  to pressure),  and  gravity.   The  cross sectional  area  δA is very  small and  the variation  of pressure  over it therefore negligible.  Let the pressure  at the end P be p and that at the end Q be p + δp.  The  force on the end P is therefore pδA and  the force on the end  Q  is (p + δp)δA.   If the length  of the cylinder  is δl  its  volume  is δAδl  and  its weight gρδAδl where ρ represents the density and g the acceleration due to gravity.  Since no shear  forces are involved  in a fluid at rest,  the only forces acting  on the sides of the cylinder are perpendicular to them and therefore have no component along the axis.  For equilibrium,  the algebraic  sum of the forces in any direction  must be zero.  Resolving in the direction QP:

(p + δp)δA + gρδAδl cos Θ = 0                 (1)

Now if P is at a height  z above  some suitable  horizontal  datum plane  and  Q is at height  z + δz, then the vertical  difference in level between  the ends of the cylinder  is δz and δl cos Theta = δz. Equation (1) therefore simplifies to

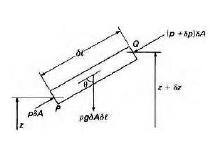
Figure  1:

and in the limit as δz → 0

The  minus  sign indicates  that the pressure  decreases  in the direction  in which z in- creases, that is, upwards.  If P and Q are in the same horizontal plane, then δz = 0, and consequently δp is also zero whatever the value of ρ. Then, in any fluid in equilibrium,  the pressure  is  the same at any  two  points  in the same horizontal plane , provided that they can be connected by a line in that plane and wholly in the fluid. In other words, a surface of equal pressure  (an isobar)  is a horizontal plane.

A further deduction is possible from (3).  If everywhere  in a certain  horizontal  plane the pressure is p, then in another horizontal plane, also in the fluid and at a distance δz above, the pressure will be p+∂p/δz. Since this pressure also must be constant throughout a hor- izontal plane, it follows that there is no horizontal variation in  ∂p/δz , and so, by (3), neither does ρg vary horizontally.  For a homogeneous incompressible fluid this is an obvious truth because  the density  is the same everywhere  and  g does not vary  horizontally.   But the result  tells  us that a condition  for equilibrium  of any  fluid is that the  density  as well as the pressure must be constant over any horizontal plane . This is a foundation for the law of connected (communicating) vessels.

The  pressure  on  the horizontal  plane  that goes through  the to vessels which  are  connected, that it is means that to different points one can to join by the curve that always stay with the same fluid, is the same.

This  is why  immiscible  fluids of different  densities  have  a  horizontal  interface  when they are in equilibrium.

There  are, then, three conditions for equilibrium  of any fluid:

1. The pressure  must be the same over any horizontal plane;
2. The density must be the same over any horizontal plane;
3.  The pressure varies only in the vertical z direction as dp/dz =−gρ
   

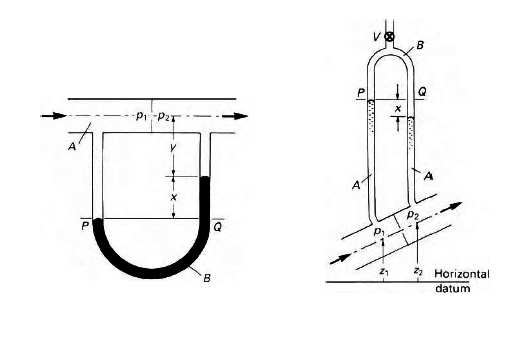
Figure  2: The pressures  by virtu of the connected vessels law, at the points P and Q are the same.  On the left U-tube manometer, on the right inverted U-tube manometer.