Learn about Energy

Energy can be defined as the capacity to do work. Energy can manifest itself in many forms like mechanical energy, thermal energy, electric energy, chemical energy, light energy, nuclear energy, etc. The energy possessed by a body due to its position or due to its motion is called mechanical energy. The mechanical energy of a body consists of potential energy and kinetic energy.

Potential energy
The potential energy of a body is the energy stored in the body by virtue of its position or the state of strain. Hence water stored in a reservoir, a wound spring, compressed air, stretched rubber chord, etc, possess potential energy. Potential energy is given by the amount of work done by the force acting on the body, when the body moves from its given position to some other position.

Expression for the potential energy
Let us consider a body of mass m, which is at rest at a height h above the ground as shown in Fig below. The work done in raising the body from the ground to the height h is stored in the body as its potential energy and when the body falls to the ground, the same amount of work can be got back from it. Now, in order to lift the body vertically up, a force mg equal to the weight of the body should be applied.

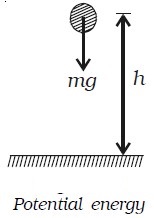
When the body is taken vertically up through a height h, then work done, W = Force × displacement
∴ W = mg × h
This work done is stored as potential energy in the body
∴ EP = mgh

Kinetic energy
The kinetic energy of a body is the energy possessed by the body by virtue of its motion. It is measured by the amount of work that the body can perform against the impressed forces before it comes to rest. A falling body, a bullet fired from a rifle, a swinging pendulum, etc. possess kinetic energy. A body is capable of doing work if it moves, but in the process of doing work its velocity gradually decreases. The amount of work that can be done depends both on the magnitude of the velocity and the mass of the body. A heavy bullet will penetrate a wooden plank deeper than a light bullet of equal size moving with equal velocity.

Expression for Kinetic energy
Let us consider a body of mass m moving with a velocity v in a straightline as shown in Fig. below. Suppose that it is acted upon by a constant force F resisting its motion, which produces retardation a (decrease in acceleration is known as retardation). Then

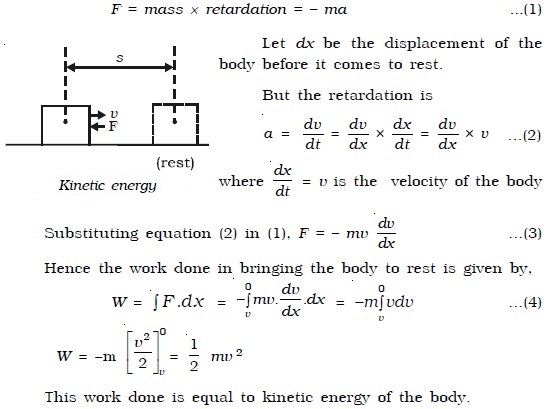
∴ Kinetic energy Ek = 1/2 mv2

Principle of work and energy (work – energy theorem) Statement
The work done by a force acting on the body during its displacement is equal to the change in the kinetic energy of the body during that displacement.
Proof
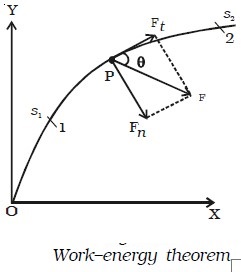
Let us consider a body of mass m acted upon by a force F and moving with a velocity v along a path as shown in Fig. below. At any instant, let P be the position of the body from the origin O. Let θ be the angle made by the direction of the force with the tangential line drawn at P.
The force F can be resolved into two rectangular components :
(i) Ft = F cos θ , tangentially and
(ii) Fn = F sin θ , normally at P.
But Ft = mat …(1)

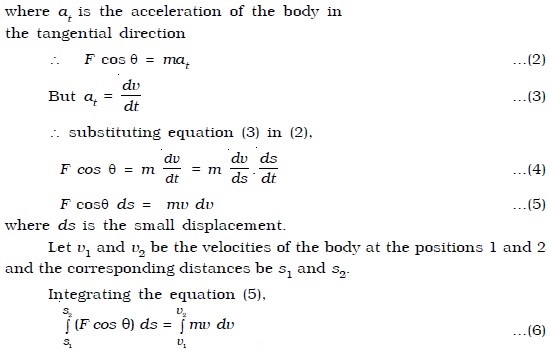
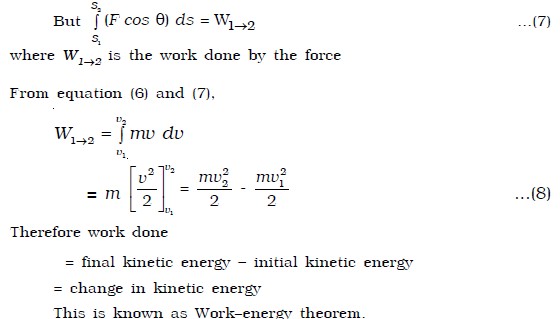
Conservative forces and non-conservative forces
Conservative forces
If the work done by a force in moving a body between two positions is independent of the path followed by the body, then such a force is called as a conservative force. Examples : force due to gravity, spring force and elastic force. The work done by the conservative forces depends only upon the initial and final position of the body.
(i.e.) ?∫→F . →dr = 0
The work done by a conservative force around a closed path is zero.

Non conservative forces
Non-conservative force is the force, which can perform some resultant work along an arbitrary closed path of its point of application. The work done by the non-conservative force depends upon the path of the displacement of the body
(i.e.) ?∫ →F . →dr ≠ 0
(e.g) Frictional force, viscous force, etc.

Law of conservation of energy
The law states that, if a body or system of bodies is in motion under a conservative system of forces, the sum of its kinetic energy and potential energy is constant.
Explanation
From the principle of work and energy,
Work done = change in the kinetic energy

which means that the sum of the potential energy and kinetic energy of a system of particles remains constant during the motion under the action of the conservative forces.

Power
It is defined as the rate at which work is done.
power = work done/time
Its unit is watt and dimensional formula is ML2 T–3.
Power is said to be one watt, when one joule of work is said to be done in one second.
If dw is the work done during an interval of time dt then,
power = dw/dt …(1)
But dw = (F cos θ) ds …(2)
where θ is the angle between the direction of the force and displacement. F cos θ is component of the force in the direction of the small displacement ds.