If we throw a body upwards, it reaches a certain height and then falls back. This is due to the gravitational attraction of the Earth. If we throw the body with a greater speed, it rises to a greater height. If the 161 body is projected with a speed of 11.2 km/s, it escapes from the Earth and never comes back. The escape speed is the minimum speed with which a body must be projected in order that it may escape from the gravitational pull of the planet.



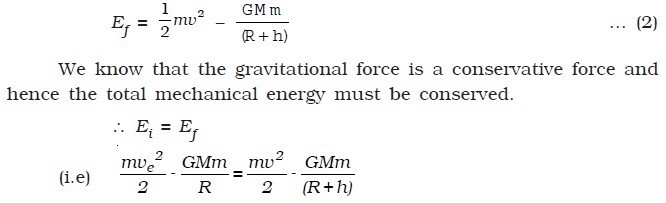
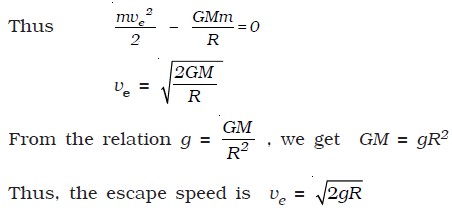
The escape speed for Earth is 11.2 km/s, for the planet Mercury it is 4 km/s and for Jupiter it is 60 km/s. The escape speed for the moon is about 2.5 km/s.

An interesting consequence of escape speed with the atmosphere of a planet
We know that the escape speed is independent of the mass of the body. Thus, molecules of a gas and very massive rockets will require the same initial speed to escape from the Earth or any other planet or moon. The molecules of a gas move with certain average velocity, which depends on the nature and temperature of the gas. At moderate temperatures, the average velocity of oxygen, nitrogen and carbon–di–oxide is in the order of 0.5 km/s to 1 km/s and for lighter gases hydrogen and helium it is in the order of 2 to 3 km/s. It is clear that the lighter gases whose average velocities are in the order of the escape speed, will escape from the moon. The gravitational pull of the moon is too weak to hold these gases. The presence of lighter gases in the atmosphere of the Sun should not surprise us, since the gravitational attraction of the sun is very much stronger and the escape speed is very high about 620 km/s.