Integration of eqn (3) for a homogeneous  fluid of constant density gives

p + gρz = const.                                                     (4)

The value of the constant in eqn.  (4) is determined by the value of p at a point where z is specified.  If the fluid is a liquid with a horizontal free surface at which the pressure  is atmospheric (pa) this free surface may be taken as the datum level z = 0. For a point at a depth h below the surface, h = −z (since h is measured  downwards  whereas z is measured upwards)  and, from eqn.  (4)

p = pa + ρgh                                                        (5)

From  the formula  (5)  it  is clear  that the pressure  increases  linearly  with  the depth, whatever the shape of any solid boundaries  may be. Equation (5) shows that the pressure at a point in a liquid in equilibrium  is due partly to the weight of the liquid.   Thus atmospheric  pressure  is usually  effective,  even if indirectly,  on all surfaces,  and  over the differences of height normally encountered it is sensibly constant.  Consequently it is often simpler  to regard  atmospheric  pressure  as  the zero  of the pressure  scale.   As we have already  mentioned  A pressure  expressed  relative  to atmospheric  pressure  is known  as a gauge pressure.  The pressure  expressed by equation

p = ρgh                                                            (6)

is named  as the hydrostatic pressure.

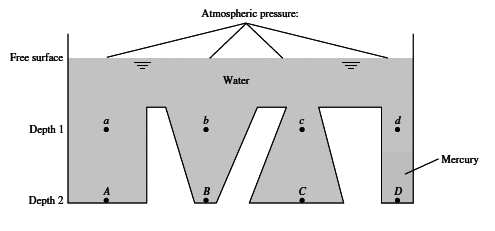
Figure  3: Hydrostatic-pressure distribution.  Points  a, b, c, and  d are at equal depths in water and therefore have identical pressures.  Points A, B, and C are also at equal depths in water and  have identical pressures  higher  than a, b, c, and  d.  Point D has a different pressure  from A, B, and C because it is not connected to them by a water path.

The direct proportionality between hydrostatic pressure  and h for a fluid of constant density  enables  the pressure  to be  simply  visualized  in  terms  of the vertical  distance h = p/ρg.   The  quotient  p/ρg  is termed  the pressure  head  corresponding  to p.  For a liquid without a free surface,  as for example  in a closed pipe, p/ρg corresponds  to the height above the pipe to which a free surface would rise if a small vertical tube of sufficient length  and  open to atmosphere   known  as a piezometer  tube   were connected  to the pipe