Inertia

Newton’s first law of motion states that a body remains in a state of rest or uniform motion in a straight line unless acted on by an external force. This resistance to change is referred to as the inertia of a body and the amount of inertia depends on the mass of the body. Therefore it takes a great deal more force to accelerate a fully laden heavy goods vehicle from rest than the force required to produce the same acceleration in a bicycle from rest.

Resisted motion

The following points should be carefully noted when using the expression F = ma:

• F can refer to both an accelerating force or a retarding force.
• It is often necessary to determine the value of an acceleration or a retardation, using the equations of motion considered earlier, when working out engineering calculations.
• When a force causing the acceleration of a body is resisted by a force trying to retard (decelerate) the body, the body is said to be subject to resisted motion.

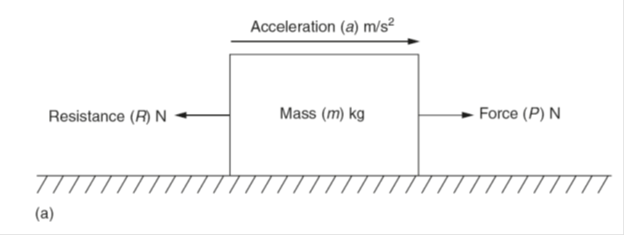
Figure 1(a) shows a force P acting on a mass m against a resistance R and producing an acceleration a. The accelerating force F_a = (P – R) and F_a = ma is written P – R = ma.

Figure 1(b) shows a suspended body of mass m. Let P be the tension in the rope suspending the body:

1. For motion up or down at constant speed, or when the body is at rest, the acceleration equals zero therefore the accelerating force (F) also equals zero.
2. For motion downwards with acceleration a, W is greater than P where W = mg. Then

the accelerating force F = (W – P) so that (W – P) = ma.

3. For motion upwards with acceleration a, F = (P – W ) so that (P – W) = ma.

Figure 1(c) shows a body on a smooth inclined plane. For this example any friction will be ignored. The component force of weight W acting down the plane = W sin θ, where W = mg (N):

1. If P is greater than W sin θ, the body moves up the plane with acceleration a. The accelerating force F = P – W sin θ so that P – W sin θ = ma.
2. If W sin θ is greater than P, the body moves down the plane with acceleration a. Then the accelerating force F = W sin θ – P so that W sin θ – P = ma.

 Example

A body of mass of 600 kg has a resistance to motion of 400 N. Determine the total force to be applied to the body to produce a uniform acceleration of 3 m/s.

Let the total force required = P.

Then: The accelerating force F = (P – 400)

Since F = ma Then: (P – 400 N) = 600 kg × 3m/s

Therefore: P = 400 N + 1800 N = 2200N

 Example

A passenger lift of mass 1500 kg starts from rest and reaches an upward velocity of 5 m/s in a distance of 10 m. Determine the tension in the lift cable if the acceleration is constant. Take g = 9.81 m/s².

To find the acceleration use the expression (v₂)² = (v₁)² + 2as

 Therefore:

5²m/s = 0 + 2 m/s ×. a ×10m

So:

a = 25/(2 ×10) = 1.25 m/s²

Whilst the lift is stationary, the tension in the cable is only due to the force of gravity acting on the lift (mg) which is equal to 1500 kg × 9.81 m/s² = 14715 N. Since the lift is accelerating upwards the tension P is greater than 14715 N.

Let P = the tension in the lift cable.

Then, the accelerating force F = P – 14715 = ma = 1500 × 1.25 m/s².

Therefore: P = 14715 + 1500 × 1.25 = 16590 N = 16.59 kN.