Kinematics
Kinematics is the study of the motion of bodies without considering the forces necessary to produce the motion. Linear velocity is the rate of change of displacement with respect to time and can be expressed as:

Velocity =ds/dt
Remember that the velocity of a body is its speed in a prescribed direction. The numerical values of speed and velocity are identical. Displacement is the area under a velocity–time graph. Since:

v = ds/dt then  =

Similarly, linear acceleration equals the rate of change of linear velocity:

Acceleration = rate of change of velocity/time = dv/dt or d²s/dt²

Note how acceleration is also the second derivative of distance and time. Velocity is the area under an acceleration–time graph. Since:
a = dv/dt then  =

Similarly angular acceleration equals the rate of change of angular velocity.
α= dω/dt or α =d₂θ/dt²

 Ballistics
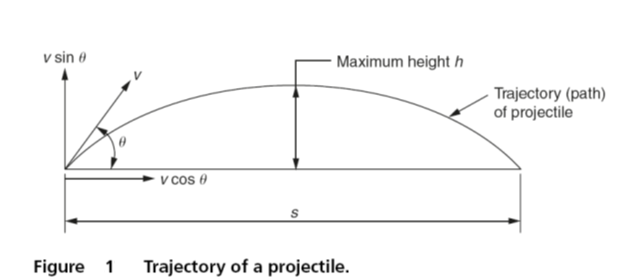
Figure 1 shows the trajectory of a projectile fired from a gun with an elevation of θ and an initial velocity of v₁ m/s. The vertical component of the force v_v = v₁ sin θ and the horizontal component of the force v_H = v₁ cos θ. Ignoring the air resistance, the only force acting on the projectile will be the gravitational acceleration (9.81 m/s²) acting on the mass of the projectile in a downwards direction. Since there is no horizontal force acting on the projectile the projection velocity remains constant throughout its flight. (In reality it would be progressively slowed up by the air resistance.)

From the relationships, the total time of flight can be obtained by using the expression s = v₁t  + 1⁄2at². Since the projectile is assumed to start from ground level, attain a maximum height of h as shown and return to ground level so that the net vertical distance travelled will be zero. Therefore:

s = 0, v_V =v₁ sin θ and a =-g.

Since:

0 = (v₁ sin θ) t – gt² then t (2v₁ sinθ)/g

Since the horizontal component of the velocity of the projectile remains constant, the horizontal distance s travelled (the range) by the projectile can be calculated as follows:

The distance travelled or range(s) = horizontal component of velocity × time of flight.
s = (v₁ cos θ) × (2v₁ sin θ)/g = [(v₁)² sin 2θ]/g (since: sin 2θ = 2 sinθ cos θ)

The maximum height (h) reached during the flight of the projectile can be obtained from the expression:

h = [(v₁)² sin²2θ]/2g