Kinetics
Kinetics
Is the study of forces that cause motion as distinct from kinetics which is the study of the geometry of motion. Therefore kinematics is the application on Newton’s laws of motion.
Universal gravitation
The law governing the mutual attraction between bodies possessing mass is known as the law of universal gravitation. This law was postulated by Sir Isaac Newton and it states that every body in the universe is attracted to every other body by a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance separating them. Stated mathematically:
F = (Gm1m2)/d2
Where:
F = mutual force of attraction between masses m1 and m2
d = distance between the masses
G = the gravitational constant (independent of the masses involved)
For any two masses on any planet, including planet earth, the mutually attractive force F between them is negligible compared with the force between each mass and the planet on which they are resting. Since planet earth exerts a force on all other bodies it follows from Newton’s second law of motion that this force will produce an acceleration g m/s2.
Since:
(GM0M)/r = F = Mg
Therefore:
g = (GM0)/r = 9.81 m/s2
Where:
G = gravitational constant (6.668 × 10-11m3/kg s2)
M0 = mass of planet earth (5.98 × 1024 kg) assumed to be concentrated at the centre of the planet.
r = mean radius of planet earth (6.375 × 106m)
g = mean gravitational acceleration of planet earth
F = mutual force of attraction
Linear translation
Any body acted upon by a number of external forces so that the resultant of these forces passes through the centre of the mass of the body then the resulting motion will be translatory. Further, since the resultant force acts through the centre of the mass it will have no moment and the body will not rotate. Therefore any such motion will be translatory and will move or tend to move the body from one place to another in a straight line.
Translation in a curved path
When a body moves in a curved path of radius r and at a uniform speed v it is subject to an inward radial acceleration of v2/r. This is known as the centripetal acceleration. Newton’s second law of motion states that a body cannot be accelerated unless it is subjected to an external force. Thus:
Centripetal force = mass × centripetal acceleration =(mv2)/r
Since v = rω for uniform circular motion, the centripetal force =mω2r
The centripetal force must be applied externally to the body for example, in the case of a car, by the friction of the tyres in contact with the road or, in the case of a railway rain by the side-thrust of the rails on the flanges of the wheels of the rolling stock. Newton’s third law states that there is a reactive force equal and opposite to every active force. Therefore there must be an equal and opposite force to the centripetal force. This is the centrifugal force and it acts radially outwards. In the case of the car the car pushes outwards against the road surface (centrifugal force) and the road pushes back against the tyres of the car (centripetal force) unless the friction force between the tyres and the road breaks down, then the car will skid.
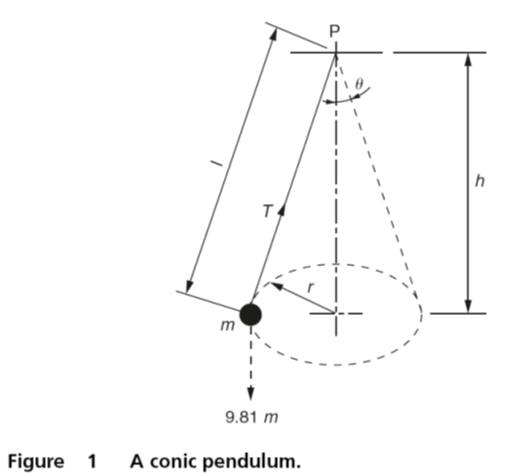
Conic pendulum
If a mass m is suspended from a pivot P by an arm of length l so that it rotates around a circular path of radius r at a constant velocity ω, as shown in Fig. 1, then for any specific speed of rotation the inclination of the arm θ and the radius of rotation r will have definite and inter-related values. This is the principle of the conical pendulum and also the principle of the governor used to control the speed of engines. In the latter case if the load on the engine decreased so that the engine speed started to rise, then r and θ would tend to increase and the linkage to which the mass m was attached would close the throttle valve so that the engine speed would be reduced to the normal (safe) value.
Conversely if the load increased so that the engine started to slow down then r and θ would reduce and the linkage to which the mass m was attached would open the throttle and bring the engine back to its correct operating speed. Thus the engine would tend to run at a constant speed.
Let T be the tension in the link supporting the mass m, then the centripetal force to maintain circular motion is provided by horizontal component force of T.
The horizontal component force of T is:
T sinθ= mrω2
The vertical component force of T for equilibrium is:
T cosθ = 9.81m
Since:
sinθ/cosθ = tanθ
Then:
tanθ = (rω2)/9.81
Since:
tanθ = (rω2)/9.81 and tanθ= r/h then r/h= (rω2)/9.81
Therefore:
h = 9.81/ω2
r = l sinθ
l = r/sinθ
T = m/ω2
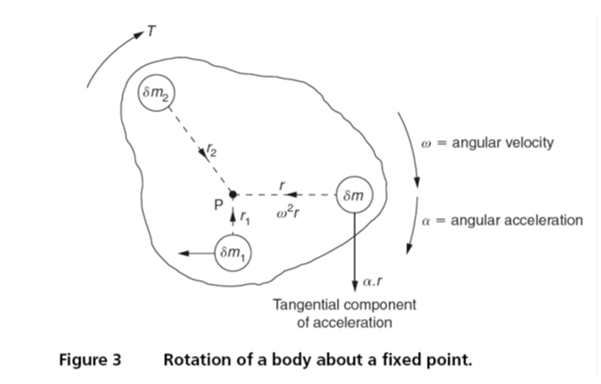
Rotation of a body about a fixed axis
When a body only possesses linear translatory motion, the resultant of the external forces acting on that body will pass through the centre of mass and rotation cannot occur. However when the resultant force does not pass through the centre of mass of the body a turning moment will be present and the body will rotate. Figure 3 shows a body subjected to a torque T so that it rotates about the pivot point P. The instantaneous angular velocity of the body is ω and its angular acceleration is α.
The elemental masses δm, δm1 and δm2 are each subjected to two acceleration components, a tangential component α r and a centripetal component ω 2r which passes through the pivot point P about which the body rotates. Since the centripetal component for each elemental mass passes through the pivot point P there can be no moment about this point. However the component acting tangentially on each elemental mass (δm. α r2) about P does provide a turning moment. Therefore the total turning moment about the pivot point P is:
∑(δm α.r2) = α ∑(δm.r2) since all the elements rotate about P at the same speed.
∑(δm.r2) being the sum of all the elemental terms (mass × radius2) about P is called the moment of inertia. Thus:
The moment of inertia IP =∑(δm.r2) and the turning moment T about P = IP α.
The units are: T (Nm), IP (kg m2) and α (rad/s2).
Radius of gyration
Since the sum of the elemental masses equals the total mass of a body (m =∑δm) and if k is the distance from the chosen axis at which the total mass is assumed to be concentrated, then mk2 =∑(δm.r2) then the moment of inertia can be expressed as:
IP = mk2 where k is the radius of gyration about the specified axis of rotation.
Centre of percussion
It is often necessary, in rotational problems, to identify the line of action of the resultant force F (as shown in Fig 4) where F equals the mass of the body multiplied by the acceleration of the centre of mass. It is assumed that this resultant force F passes through some point P on the line RGP where R is the axis of rotation and G is the centre of mass. The tangential component of the force F can produce a turning moment about R. P is at a position in a body where the moments of all the external forces balance out and equal zero. The point P is known as the centre of percussion. In cases where the body rotates about its centre of mass (R and G are coincident)
Then:
Torque T = m(kG)2 α = IG α
where kG is radius of gyration about G.
When a body rotates about an axis passing through its centre of mass the radius of gyration is at a minimum and, hence, the torque required to rotate the body is a minimum.
Angular momentum
The linear momentum of a body was its mass multiplied by its linear velocity. The angular momentum of a rotating body is the moment of its linear momentum about the point of rotation. Figure 5 shows a body rotating about the pivot point P with an angular velocity ω rad/s. Consider the elemental mass, δm, at a distance r from the pivot point P and whose velocity is v m/s.
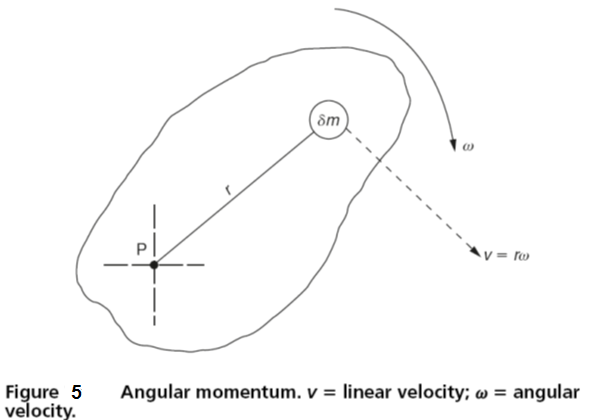
Linear momentum of the elemental mass =δm.v=δm.r ω
The moment of the linear momentum about P =r(δm.r ω) = δm.r2 ω
The moment of momentum about P for the complete body = ∑δm.r2 ω
But:
∑δm.r2 = I
Where:
I = the moment of inertia
Thus:
The angular momentum about P = I ω
Where a change of angular velocity occurs the above expression becomes:
Change in angular momentum = I(ω 2 – ω 1)
Therefore: angular impulse Tt = I(ω 2 – ω 1)
Where:
T = torque (Nm)
t = time (duration of impulse in seconds)
The kinetic energy stored in a rotating body =IP ω 2
Where: IP = moment of inertia about the pivot point P.
The kinetic energy stored in a body possessing both rotation and translation
= the kinetic energy of rotation + the kinetic energy of translation
= 1⁄2I ω 2 + 1⁄2mv2

