Mensuration Plane figures

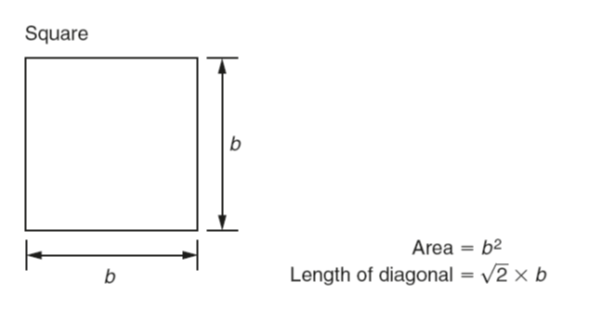
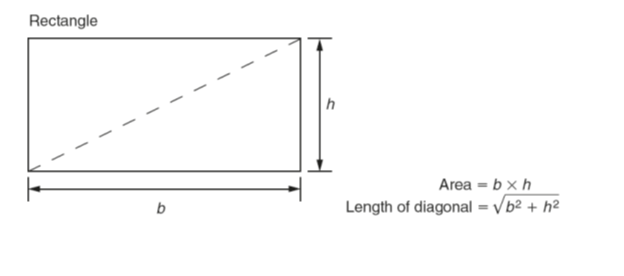
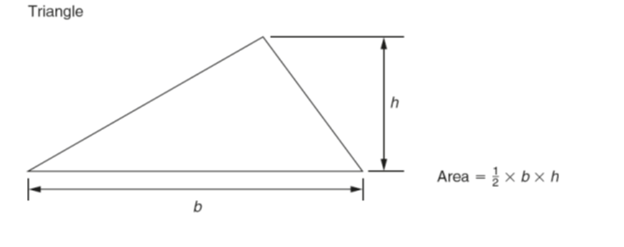
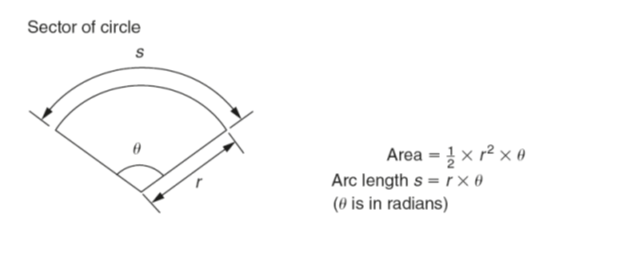
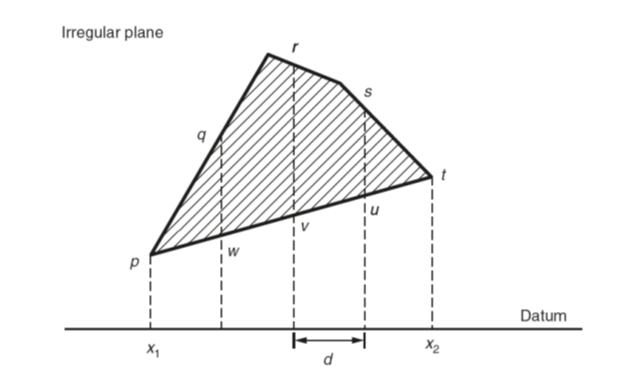
Several methods are used to find the shaded area, such as the mid-ordinate rule, the trapezoidal rule and Simpson’s rule. As an example of these, Simpson’s rule is as shown above.

Divide x1x2 into an even number of equal parts of width d.

Let p, q, r, … be the lengths of vertical lines measured from some datum, and let A be the approximate area of the irregular plane, shown shaded. Then:

A = d/3[(p+t) + 4(q+s)+2r] – d/3[(p+t)+ 4(u+w)+2r]

In general, the statement of Simpson’s rule is:

Approximate Area= (d/3) ×[(first+last)+4(sum of evens)+ 2(sum of odds)]

where first, last, evens, odds refer to ordinate lengths and d is the width of the equal parts of the datum line.

Solid objects

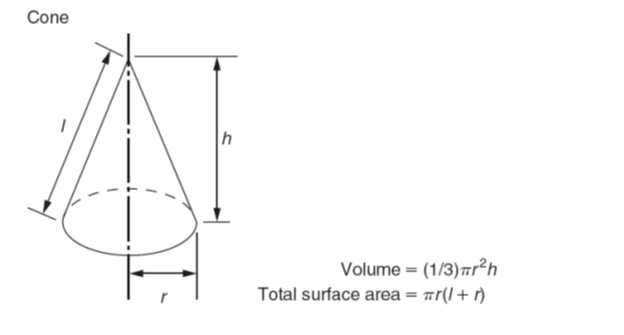
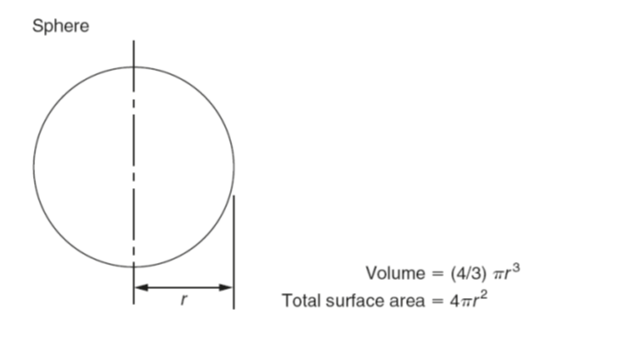
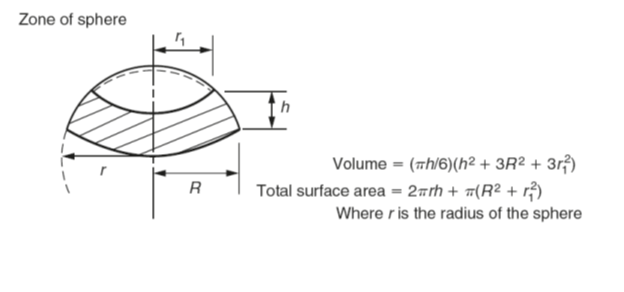
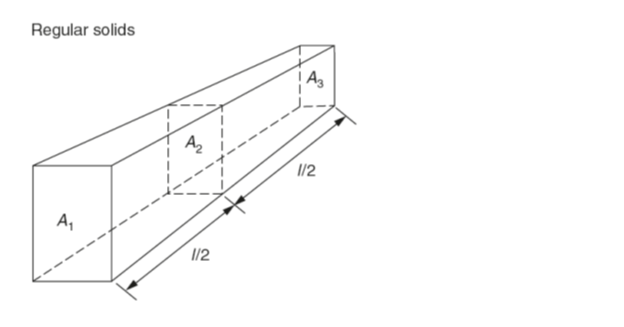
The volume of any regular solid can be found by using the prismoidal rule. Three parallel planes of areas A1, A3 and A2 are considered to be at the ends and at the centre of the solid, respectively. Then:

Volume=(l/6)(A₁+4A₂+A₃)

Where:

l is the length of the solid.

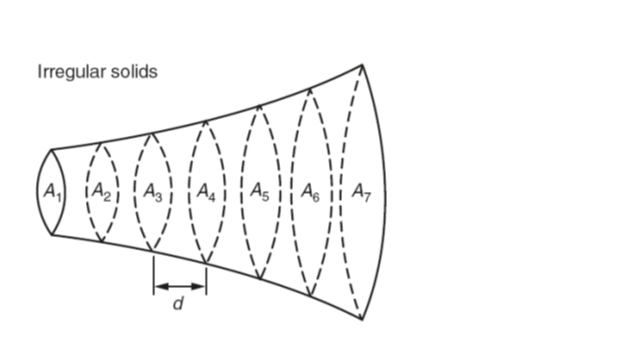
Various methods can be used to determine volumes of irregular solids; one of these is by applying the principles of Simpson’s rule (see earlier this section). The solid is considered to be divided into an even number of sections by equally spaced, parallel planes, distance d apart and having areas of A1, A2, A3, ….

Assuming, say, seven such planes, then approximate volume = (d/3) [(A₁+A₇) +4(A₂ +A₄ +A₆) +2(A₃ +A₅)].