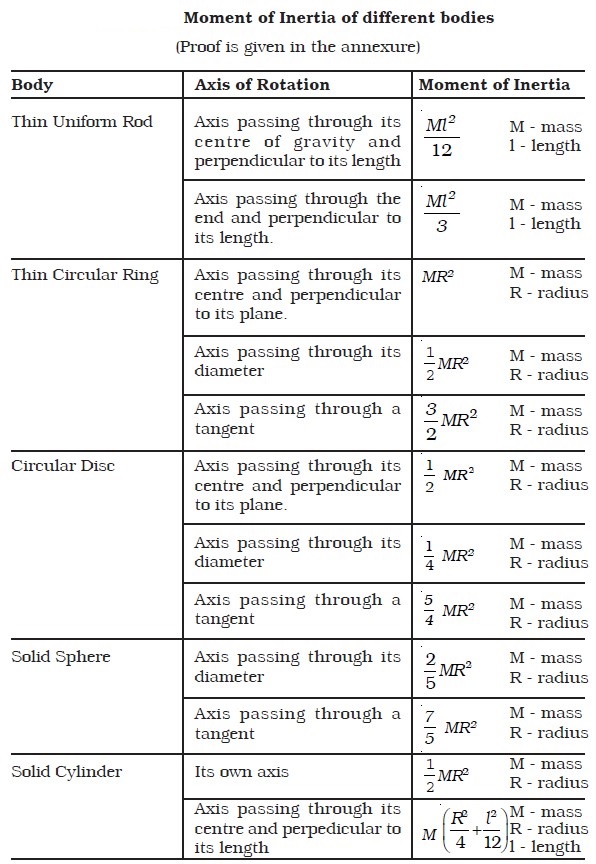
Moment of inertia and its physical significance
According to Newton’s first law of motion, a body must continue in its state of rest or of uniform motion unless it is compelled by some
external agency called force. The inability of a material body to change its state of rest or of uniform motion by itself is called inertia. Inertia is the fundamental property of the matter. For a given force, the greater the mass, the higher will be the opposition for motion, or larger the inertia. Thus, in translatory motion, the mass of the body measures the coefficient of inertia. Similarly, in rotational motion also, a body, which is free to rotate about a given axis, opposes any change desired to be produced in its state. The measure of opposition will depend on the mass of the body and the distribution of mass about the axis of rotation. The coefficient of inertia in rotational motion is called the moment of inertia of the body about the given axis. Moment of inertia plays the same role in rotational motion as that of mass in translatory motion. Also, to bring about a change in the state of rotation, torque has to be applied.
Rotational kinetic energy and moment of inertia of a rigid body
Consider a rigid body rotating with angular velocity ω about an axis XOX′. Consider the particles of masses m1, m2, m3… situated at distances r1, r2, r3… respectively from the axis of rotation. The angular velocity of all the particles is same but the particles rotate with different linear velocities. Let the linear velocities of the particles be v1,v2,v3 … respectively.


It shows that moment of inertia of a body is equal to twice the kinetic energy of a rotating body whose angular velocity is one radian per second. The unit for moment of inertia is kg m2 and the dimensional formula is ML2.
Radius of gyration
The moment of inertia of the rotating rigid body is,
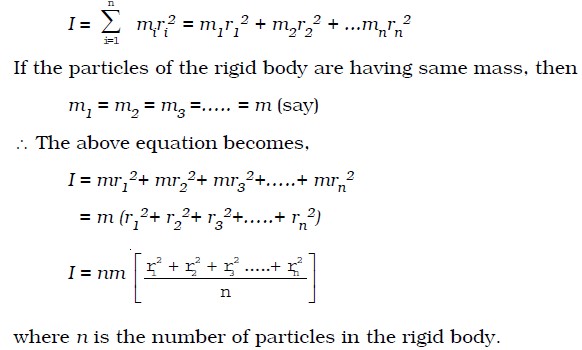
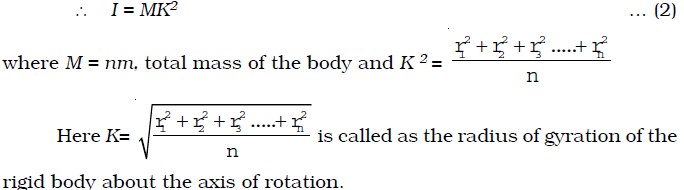
The radius of gyration is equal to the root mean square distances of the particles from the axis of rotation of the body. The radius of gyration can also be defined as the perpendicular distance between the axis of rotation and the point where the whole weight of the body is to be concentrated. Also from the equation (2) K2 = I/M (or) K = √I/M
Theorems of moment of inertia
Parallel axes theorem
Statement
The moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its centre of gravity and the product of the mass of the body and the square of the distance between the two axes.
Proof
Let us consider a body having its centre of gravity at G as shown in Fig. below. The axis XX′ passes through the centre of gravity and is
perpendicular to the plane of the body. The axis X1X1′ passes through the point O and is parallel to the axis XX′ . The distance between the two parallel axes is x.
Let the body be divided into large number of particles each of mass m . For a particle P at a distance r from O, its moment of inertia about the axis X1OX1′ is equal to m r 2. The moment of inertia of the whole body about the axis X1X1′ is given by, I0 = Σ mr2 …(1)
From the point P, drop a perpendicular PA to the extended OG and join PG.
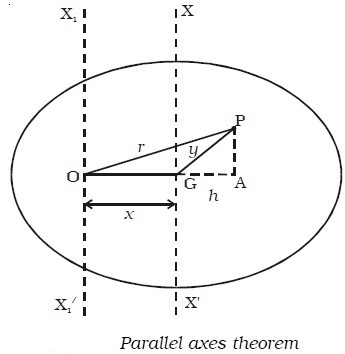
In the ΔOPA,
OP 2 = OA2 + AP 2
r2 = (x + h)2+AP 2
r2 = x2 + 2xh + h2 + AP2 …(2)
But from Δ GPA,
GP 2 = GA2 + AP 2
y 2 = h 2 + AP 2 …(3)
Substituting equation (3) in (2),
r 2 = x 2 + 2xh + y 2 …(4)
Substituting equation (4) in (1),
Io = Σ m (x2 + 2xh + y2)
= Σmx2 + Σ2mxh + Σmy2
= Mx2 + My2 + 2xΣmh …(5)
Here My2 = IG is the moment of inertia of the body about the line passing through the centre of gravity. The sum of the turning moments of all the particles about the centre of gravity is zero, since the body is balanced about the centre of gravity G.
Σ (mg) (h) = 0 (or) Σ mh = 0 [since g is a constant] …(6)
∴ equation (5) becomes, I0 = Mx2 + IG …(7)
Thus the parallel axes theorem is proved.
Perpendicular axes theorem
Statement
The moment of inertia of a plane laminar body about an axis perpendicular to the plane is equal to the sum of the moments of inertia about two mutually perpendicular axes in the plane of the lamina such that the three mutually perpendicular axes have a common point of intersection.
Proof
Consider a plane lamina having the axes OX and OY in the plane of the lamina as shown Fig. below. The axis OZ passes through O and is
perpendicular to the plane of the lamina. Let the lamina be divided into a large number of particles, each of mass m. A particle at P at a distance r from O has coordinates (x,y).
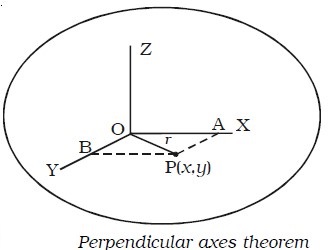
∴r2 = x2+y2 …(1)
The moment of inertia of the particle P about the axis OZ = m r2.
The moment of inertia of the whole lamina about the axis OZ is
Iz = Σmr2 …(2)
The moment of inertia of the whole lamina about the axis OX is
Ix =Σ my 2 …(3)
Similarly, Iy = Σ mx 2 …(4)
From eqn. (2), Iz = Σmr2 = Σm(x2+y2)
Iz =Σmx2+Σmy2 = Iy+ Ix
∴ Iz = Ix+ Iy
which proves the perpendicular axes theorem.