Various philosophers studied the basic ideas of cause of motion. According to Aristotle, a constant external force must be applied continuously to an object in order to keep it moving with uniform velocity. Later this idea was discarded and Galileo gave another idea on the basis of the experiments on an inclined plane. According to him, no force is required to keep an object moving with constant velocity. It is the presence of frictional force that tends to stop moving object, the smaller the frictional force between the object and the surface on which it is moving, the larger the distance it will travel before coming to rest. After Galileo, it was Newton who made a systematic study of motion and extended the ideas of Galileo. Newton formulated the laws concerning the motion of the object. There are three laws of motion. A deep analysis of these laws lead us to the conclusion that these laws completely define the force. The first law gives the fundamental definition of force; the second law gives the quantitative and dimensional definition of force while the third law explains the nature of the force.

Newton’s first law of motion
It states that every body continues in its state of rest or of uniform motion along a straight line unless it is compelled by an external force to
change that state. This law is based on Galileo’s law of inertia. Newton’s first law of motion deals with the basic property of matter called inertia and the definition of force. Inertia is that property of a body by virtue of which the body is unable to change its state by itself in the absence of external force.

The inertia is of three types
● Inertia of rest
● Inertia of motion
● Inertia of direction.

Inertia of rest
It is the inability of the body to change its state of rest by itself.

Examples
● A person standing in a bus falls backward when the bus suddenly starts moving. This is because, the person who is initially at rest continues to be at rest even after the bus has started moving.
● A book lying on the table will remain at rest, until it is moved by some external agencies.
● When a carpet is beaten by a stick, the dust particles fall off vertically downwards once they are released and do not move along the carpet and fall off.

Inertia of motion
Inertia of motion is the inability of the body to change its state of motion by itself.

Examples
● When a passenger gets down from a moving bus, he falls down in the direction of the motion of the bus.
● A passenger sitting in a moving car falls forward, when the car stops suddenly.
● An athlete running in a race will continue to run even after reaching the finishing point.

Inertia of direction
It is the inability of the body to change its direction of motion by itself.

Examples
When a bus moving along a straight line takes a turn to the right, the passengers are thrown towards left. This is due to inertia which makes the passengers travel along the same straight line, even though the bus has turned towards the right. This inability of a body to change by itself its state of rest or of uniform motion along a straight line or direction, is known as inertia. The inertia of a body is directly proportional to the mass of the body. From the first law, we infer that to change the state of rest or uniform motion, an external agency called, the force is required. Force is defined as that which when acting on a body changes or tends to change the state of rest or of uniform motion of the body along a straight line. A force is a push or pull upon an object, resulting the change of state of a body. Whenever there is an interaction between two objects, there is a force acting on each other. When the interaction ceases, the two objects no longer experience a force. Forces exist only as a result of an interaction. There are two broad categories of forces between the objects, contact forces and non–contact forces resulting from action at a distance. Contact forces are forces in which the two interacting objects are physically in contact with each other.
Tensional force, normal force, force due to air resistance, applied forces and frictional forces are examples of contact forces. Action-at-a-distance forces (non- contact forces) are forces in which the two interacting objects are not in physical contact which each other, but are able to exert a push or pull despite the physical separation. Gravitational force, electrical force and magnetic force are examples of non- contact forces.

Momentum of a body
It is observed experimentally that the force required to stop a moving object depends on two factors: (i) mass of the body and (ii) its velocity
A body in motion has momentum. The momentum of a body is defined as the product of its mass and velocity. If m is the mass of the body and v, → its velocity, the linear momentum of the body is given by →p = m→v. Momentum has both magnitude and direction and it is, therefore, a vector quantity. The momentum is measured in terms of kg m s − 1 and its dimensional formula is MLT−1. When a force acts on a body, its velocity changes, consequently, its momentum also changes. The slowly moving bodies have smaller momentum than fast moving bodies of same mass. If two bodies of unequal masses and velocities have same momentum, then,

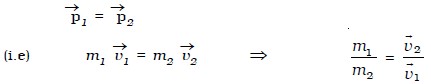
Hence for bodies of same momenta, their velocities are inversely proportional to their masses.

Newton’s second law of motion
Newton’s first law of motion deals with the behaviour of objects on which all existing forces are balanced. Also, it is clear from the first law of motion that a body in motion needs a force to change the direction of motion or the magnitude of velocity or both. This implies that force is such a physical quantity that causes or tends to cause an acceleration. Newton’s second law of motion deals with the behaviour of objects on which all existing forces are not balanced. According to this law, the rate of change of momentum of a body is directly proportional to the external force applied on it and the change in momentum takes place in the direction of the force.
If →p is the momentum of a body and →F the external force acting on it, then according to Newton’s second law of motion,


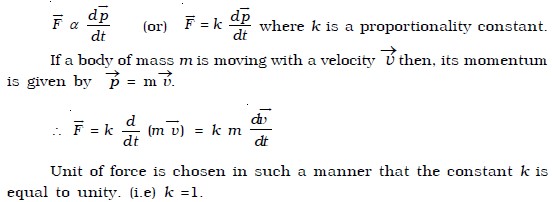
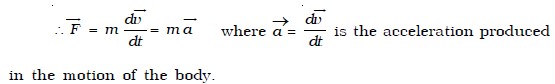
The force acting on a body is measured by the product of mass of the body and acceleration produced by the force acting on the body. The second law of motion gives us a measure of the force. The acceleration produced in the body depends upon the inertia of the body (i.e) greater the inertia, lesser the acceleration. One newton is defined as that force which, when acting on unit mass produces unit acceleration. Force is a vector quantity. The unit of force is kg m s−2 or newton. Its dimensional formula is MLT−2.

Impulsive force and Impulse of a force
Impulsive Force
An impulsive force is a very great force acting for a very short time on a body, so that the change in the position of the body during the time
the force acts on it may be neglected.
(e.g.) The blow of a hammer, the collision of two billiard balls etc.
Impulse of a force
The impulse J of a constant force F acting for a time t is defined as the product of the force and time.
(i.e) Impulse = Force × time
J = F × t
The impulse of force F acting over a time interval t is defined by the integral,
J = 0∫t F dt ….(1)

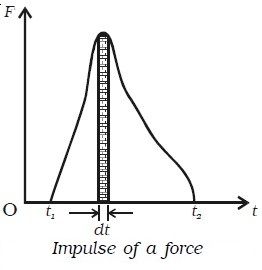
The impulse of a force, therefore can be visualised as the area under the force versus time graph as shown in Fig. above. When a variable force acting for a short interval of time, then the impulse can be measured as,
J = F average × dt …(2)
Impulse of a force is a vector quantity and its unit is N s.

Principle of impulse and momentum
By Newton’s second law of motion, the force acting on a body = m a where m = mass of the body and a = acceleration produced
The impulse of the force = F × t = (m a) t If u and v be the initial and final velocities of the body then,
a = (v – u)/t.
Therefore, impulse of the force = m * (v-u)/t *t = m(v-u) = mv-mu
Impulse = final momentum of the body
– initial momentum of the body.
(i.e) Impulse of the force = Change in momentum
The above equation shows that the total change in the momentum of a body during a time interval is equal to the impulse of the force acting during the same interval of time. This is called principle of impulse and momentum.

Examples
● A cricket player while catching a ball lowers his hands in the direction of the ball. If the total change in momentum is brought about in a very short interval of time, the average force is very large according to the equation, F =mv – mu/t
By increasing the time interval, the average force is decreased. It is for this reason that a cricket player while catching a ball, to increase
the time of contact, the player should lower his hand in the direction of the ball , so that he is not hurt.
● A person falling on a cemented floor gets injured more where as a person falling on a sand floor does not get hurt. For the same
reason, in wrestling, high jump etc., soft ground is provided.
● The vehicles are fitted with springs and shock absorbers to reduce jerks while moving on uneven or wavy roads.

Newton’s third Law of motion
It is a common observation that when we sit on a chair, our body exerts a downward force on the chair and the chair exerts an upward
force on our body. There are two forces resulting from this interaction: a force on the chair and a force on our body. These two forces are called action and reaction forces. Newton’s third law explains the relation between these action forces. It states that for every action, there is an equal and opposite reaction. (i.e.) whenever one body exerts a certain force on a second body, the second body exerts an equal and opposite force on the first. Newton’s third law is sometimes called as the law of action and reaction. Let there be two bodies 1 and 2 exerting forces on each other. Let the force exerted on the body 1 by the body 2 be →F 12 and the force exerted on the body 2 by the body 1 be →F 21. Then according to third law, →F 12 = –→F 21. One of these forces, say →F 12 may be called as the action whereas the other force →F 21 may be called as the reaction or vice versa. This implies that we cannot say which is the cause (action) or which is the effect (reaction). It is to be noted that always the action and reaction do not act on the same body; they always act on different bodies. The action and reaction never cancel each other and the forces always exist in pair. The effect of third law of motion can be observed in many activities in our everyday life. The examples are
● When a bullet is fired from a gun with a certain force (action), there is an equal and opposite force exerted on the gun in the backward direction (reaction).
● When a man jumps from a boat to the shore, the boat moves away from him. The force he exerts on the boat (action) is responsible for its motion and his motion to the shore is due to the force of reaction exerted by the boat on him.
● The swimmer pushes the water in the backward direction with a certain force (action) and the water pushes the swimmer in the forward direction with an equal and opposite force (reaction).
● We will not be able to walk if there were no reaction force. In order to walk, we push our foot against the ground. The Earth in turn exerts an equal and opposite force. This force is inclined to the surface of the Earth. The vertical component of this force balances our weight and the horizontal component enables us to walk forward.

● A bird flies by with the help of its wings. The wings of a bird push air downwards (action). In turn, the air reacts by pushing the bird upwards (reaction).
● When a force exerted directly on the wall by pushing the palm of our hand against it (action), the palm is distorted a little because, the wall exerts an equal force on the hand (reaction).

Law of conservation of momentum
From the principle of impulse and momentum, impulse of a force, J = mv −mu
If J = 0 then mv −mu = 0 (or) mv = mu
(i.e) final momentum = initial momentum
In general, the total momentum of the system is always a constant (i.e) when the impulse due to external forces is zero, the momentum of the
system remains constant. This is known as law of conservation of momentum.
We can prove this law, in the case of a head on collision between two bodies.

Proof
Consider a body A of mass m1 moving with a velocity u1 collides head on with another body B of mass m2 moving in the same direction as A with velocity u2 as shown in Fig below.

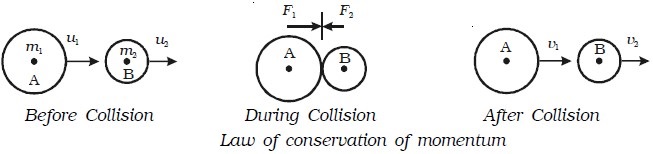
After collision, let the velocities of the bodies be changed to v1 and v2 respectively, and both moves in the same direction. During collision, each body experiences a force. The force acting on one body is equal in magnitude and opposite in direction to the force acting on the other body. Both forces act for the same interval of time.

Let F1 be force exerted by A on B (action), F2 be force exerted by B on A (reaction) and t be the time of contact of the two bodies during collision. Now, F1 acting on the body B for a time t, changes its velocity from u2 to v2.

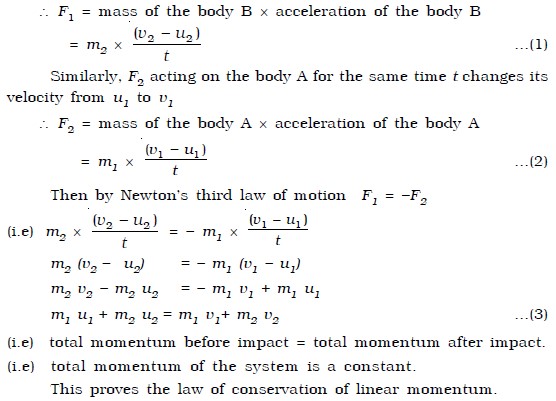
Applications of law of conservation of momentum
The following examples illustrate the law of conservation of momentum.
Recoil of a gun
Consider a gun and bullet of mass mg and mb respectively. The gun and the bullet form a single system. Before the gun is fired, both 70 the gun and the bullet are at rest. Therefore the velocities of the gun and bullet are zero. Hence total momentum of the system before firing is mg(0) + mb(0) = 0
When the gun is fired, the bullet moves forward and the gun recoils backward. Let vb and vg are their respective velocities, the total momentum of the bullet – gun system, after firing is mbvb + mgvg
According to the law of conservation of momentum, total momentum before firing is equal to total momentum after firing.
(i.e) 0 = mb vb + mg vg (or) vg = – mb/mg b
It is clear from this equation, that vg is directed opposite to vb. Knowing the values of mb, mg and vb, the recoil velocity of the gun vg can be calculated.

Explosion of a bomb
Suppose a bomb is at rest before it explodes. Its momentum is zero. When it explodes, it breaks up into many parts, each part having a particular momentum. A part flying in one direction with a certain momentum, there is another part moving in the opposite direction with the same momentum. If the bomb explodes into two equal parts, they will fly off in exactly opposite directions with the same speed, since each part has the same mass.

Applications of Newton’s third law of motion
Apparent loss of weight in a lift
Let us consider a man of mass M standing on a weighing machine placed inside a lift. The actual weight of the man = Mg. This weight (action) is measured by the weighing machine and in turn, the machine offers a reaction R. This reaction offered by the surface of contact on the man is the apparent weight of the man.
Case (i)
When the lift is at rest:
The acceleration of the man = 0
Therefore, net force acting on the man = 0
From Fig. below(i), R – Mg = 0 (or) R = Mg

That is, the apparent weight of the man is equal to the actual weight.
Case (ii)
When the lift is moving uniformly in the upward or downward direction:
For uniform motion, the acceleration of the man is zero. Hence, in this case also the apparent weight of the man is equal to the actual weight.
Case (iii)
When the lift is accelerating upwards:
If a be the upward acceleration of the man in the lift, then the net upward force on the man is F = Ma
From Fig above(ii), the net force
F = R – Mg = Ma (or) R = M ( g + a )
Therefore, apparent weight of the man is greater than actual weight.
Case (iv)
When the lift is accelerating downwards:
Let a be the downward acceleration of the man in the lift, then the net downward force on the man is F = Ma
From Fig. above(iii), the net force
F = Mg – R = Ma (or) R = M (g – a)
Therefore, apparent weight of the man is less than the actual weight. When the downward acceleration of the man is equal to the acceleration due to the gravity of earth, (i.e) a = g
∴ R = M (g – g) = 0
Hence, the apparent weight of the man becomes zero. This is known as the weightlessness of the body.

Working of a rocket and jet plane
The propulsion of a rocket is one of the most interesting examples of Newton’s third law of motion and the law of conservation of momentum. The rocket is a system whose mass varies with time. In a rocket, the gases at high temperature and pressure, produced by the
combustion of the fuel, are ejected from a nozzle. The reaction of the escaping gases provides the necessary thrust for the launching and
flight of the rocket. From the law of conservation of linear momentum, the momentum of the escaping gases must be equal to the momentum gained by the rocket. Consequently, the rocket is propelled in the forward direction opposite to the direction of the jet of escaping gases. Due to the thrust imparted to the rocket, its velocity and acceleration will keep on increasing. The mass of the rocket and the fuel system keeps on decreasing due to the escaping mass of gases.