A body thrown with some initial velocity and then allowed to move under the action of gravity alone, is known as a projectile. If we observe the path of the projectile, we find that the projectile moves in a path, which can be considered as a part of parabola. Such a motion is known as projectile motion. A few examples of projectiles are (i) a bomb thrown from an aeroplane (ii) a javelin or a shot-put thrown by an athlete (iii) motion of a ball hit by a cricket bat etc. The different types of projectiles are shown in Fig. below. A body can be projected in two ways:

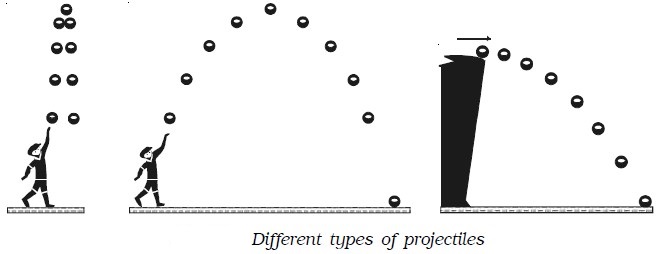
● It can be projected horizontally from a certain height.
● It can be thrown from the ground in a direction inclined to it.
The projectiles undergo a vertical motion as well as horizontal motion. The two components of the projectile motion are (i) vertical component and (ii) horizontal component. These two perpendicular components of motion are independent of each other. A body projected with an initial velocity making an angle with the horizontal direction possess uniform horizontal velocity and variable vertical velocity, due to force of gravity. The object therefore has horizontal and vertical motions simultaneously. The resultant motion would be the vector sum of these two motions and the path following would be curvilinear. The above discussion can be summarised as in the Table below

In the study of projectile motion, it is assumed that the air resistance is negligible and the acceleration due to gravity remains constant.

Angle of projection
The angle between the initial direction of projection and the horizontal direction through the point of projection is called the angle of projection.

Velocity of projection
The velocity with which the body is projected is known as velocity of projection.

Range
Range of a projectile is the horizontal distance between the point of projection and the point where the projectile hits the ground.

Trajectory
The path described by the projectile is called the trajectory.

Time of flight
Time of flight is the total time taken by the projectile from the instant of projection till it strikes the ground.

Motion of a projectile thrown horizontally
Let us consider an object thrown horizontally with a velocity u from a point A, which is at a height h from the horizontal plane OX (Fig below). The object acquires the following motions simultaneously :
● Uniform velocity with which it is projected in the horizontal direction OX
● Vertical velocity, which is non-uniform due to acceleration due o gravity.

The two velocities are independent of each other. The horizontal velocity of the object shall remain constant as no acceleration is acting in the horizontal direction. The velocity in the vertical direction shall go on changing because of acceleration due to gravity.

Path of a projectile

The above equation is the equation of a parabola. Thus the path taken by the projectile is a parabola.

Time of flight and range

Motion of a projectile projected at an angle with the horizontal (oblique projection)
Consider a body projected from a point O on the surface of the
Earth with an initial velocity u at an angle θ with the horizontal as
shown in Fig. below. The velocity u can be resolved into two components

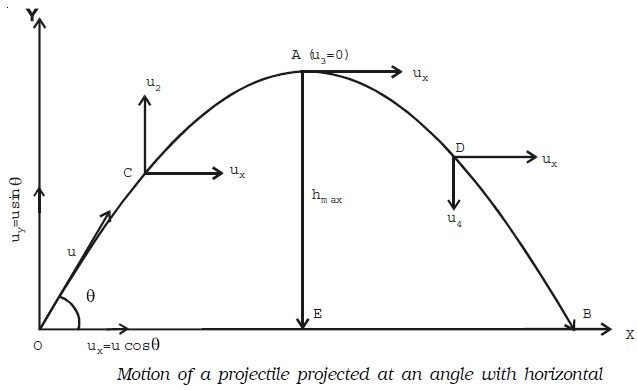
● ux = u cos θ , along the horizontal direction OX and
● uy = u sin θ, along the vertical direction OY
The horizontal velocity ux of the object shall remain constant as no acceleration is acting in the horizontal direction. But the vertical component uy of the object continuously decreases due to the effect of the gravity and it becomes zero when the body is at the highest point of its path. After this, the vertical component uy is directed downwards and increases with time till the body strikes the ground at B.

Path of the projectile
Let t1 be the time taken by the projectile to reach the point C from the instant of projection. Horizontal distance travelled by the projectile in time t1 is, x = horizontal velocity × time

The above equation is of the form y = Ax + Bx2 and represents a parabola. Thus the path of a projectile is a parabola.

Resultant velocity of the projectile at any instant t1
At C, the velocity along the horizontal direction is ux = u cos θ and the velocity along the vertical direction is uy= u2.

Maximum height reached by the projectile
The maximum vertical displacement produced by the projectile is known as the maximum height reached by the projectile. In the above Motion of a projectile projected at an angle with horizontal Fig, EA is the maximum height attained by the projectile. It is represented as hmax.

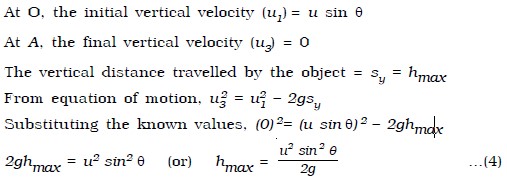
Time taken to attain maximum height
Let t be the time taken by the projectile to attain its maximum height.
From equation of motion u3 = u1 – g t
Substituting the known values 0 = u sin θ – g t
g t = u sin θ
t = u sinθ/g …(5)

Time of flight
Let tf be the time of flight (i.e) the time taken by the projectile to reach B from O through A. When the body returns to the ground, the net vertical displacement made by the projectile

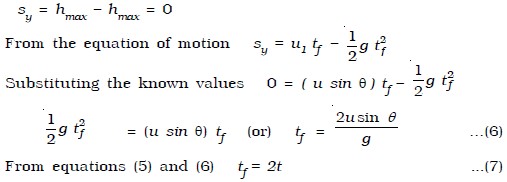
(i.e) the time of flight is twice the time taken to attain the maximum height.

Horizontal range
The horizontal distance OB is called the range of the projectile. Horizontal range = horizontal velocity × time of flight
(i.e) R = u cos θ × tf

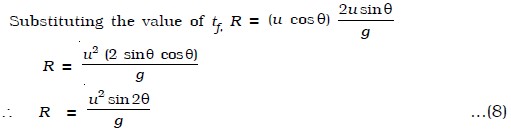
Maximum Range
From (8), it is seen that for the given velocity of projection, the horizontal range depends on the angle of projection only. The range is
maximum only if the value of sin 2θ is maximum.