Relative velocities (unconnected bodies)
The statement that a body is travelling at 50 km/h means that the body is travelling at 50 km/h relative to some other body such as the surface of planet earth. For example, an aircraft whose indicated airspeed is 300 km/h means that its airspeed is relative to the wind speed through which it is flying. The true speed of the aircraft over the ground may be greater than its airspeed if it has a following (tail) wind, or its speed over the ground will be less than its airspeed if it is flying into a headwind.

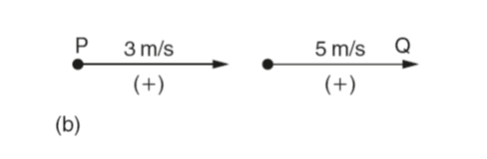
Figure 1(a) shows two unconnected bodies represented by the points P and Q. These bodies are travelling in opposite directions at 3 and 5 m/s, respectively. Assume that movement from left to right is positive and the movement from right to left is negative.

The velocity of Q relative to P = velocity Q – velocity P = (-5 m/s) – (+3 m/s) = –8 m/s

The velocity of Q relative to P is negative because the direction of Q is from right to left.

Similarly:

The velocity of P relative to Q = (+3 m/s) – (-5 m/s) = +8 m/s

The velocity of P relative to Q is positive because the direction of P is from left to right. In this explanation the choice of direction is arbitrary. The relative directions and the allocation of positive or negative values must be established at the start of each specific problem.

Since the bodies are moving in opposite directions their relative velocity is the closing velocity. Had the two bodies been moving in the same direction as shown in Fig. 1(b).
The velocity of Q relative to P=+5m/s – (+3 m/s) = +2 m/s

 If the two bodies do not travel along the same path their relative velocities cannot be determined by simple addition or subtraction. Figure 3.10(c) shows two bodies P and Q moving in different directions along different paths in the same plane. The velocity of P is v_P and the velocity of Q is v_Q.

To find the velocity of Q with respect to P it is necessary to find the apparent velocity of Q if P is stationary. To do this it is necessary to apply a velocity of –v_P to both bodies as shown in Fig. 1(d) in order to bring P to rest. From the vector diagram 1(e) it can be seen that the components of the velocity of Q are its true velocity v_Q and its superimposed velocity (-v_P). The resultant velocity of body B is represented by the vector QR which represents the velocity of Q relative to P. That is, the apparent movement of body Q as seen by an observer on body P. An observer on Q would see the body P moving in the opposite direction but with the same speed. That is, the resultant velocity vector would be reversed.

Relative velocities (connected bodies)
Unlike the previous section, this section deals with the relative velocities of bodies that are unconnected, Fig. 2(a) shows two bodies P and Q that are connected by a rigid link of length l. The velocities of the connected bodies P and Q are v_P and v_Q, respectively in the directions shown.

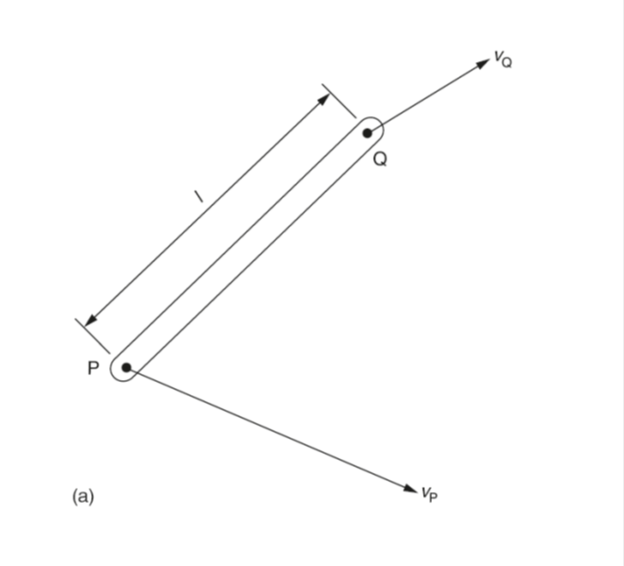
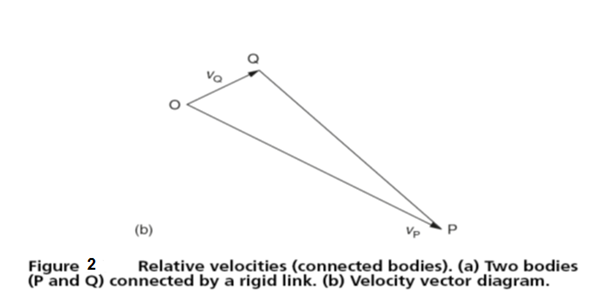
Since the distance l between the bodies P and Q is fixed, there can be no component velocity along the link connecting P and Q. Therefore any relative velocity will be perpendicular to the link connecting P and Q since this is the only direction that will not produce a component along the link connecting P and Q. The velocity vector diagram is shown in Fig. 2(b) from which it can be seen that the vector pq is perpendicular to the link connecting the bodies P and Q. Therefore P is apparently rotating with a tangential velocity pq with respect to Q. Therefore:

Angular velocity of the link = (tangential velocity)/(radius)

ω = (vector pq)/l

The velocity of Q with respect to P would give a similar result since the link connecting the bodies P and Q can have only one angular velocity.