A study of motion will involve the introduction of a variety of quantities, which are used to describe the physical world. Examples of such quantities are distance, displacement, speed, velocity, acceleration, mass, momentum, energy, work, power etc. All these quantities can be divided into two categories – scalars and vectors.
The scalar quantities have magnitude only. It is denoted by a number and unit. Examples : length, mass, time, speed, work, energy, 45 temperature etc. Scalars of the same kind can be added, subtracted, multiplied or divided by ordinary laws.
The vector quantities have both magnitude and direction. Examples: displacement, velocity, acceleration, force, weight, momentum, etc.

Representation of a vector
Vector quantities are often represented by a scaled vector diagrams. Vector diagrams represent a vector by the use of an arrow drawn to scale in a specific direction. An example of a scaled vector diagram is shown in Fig below.

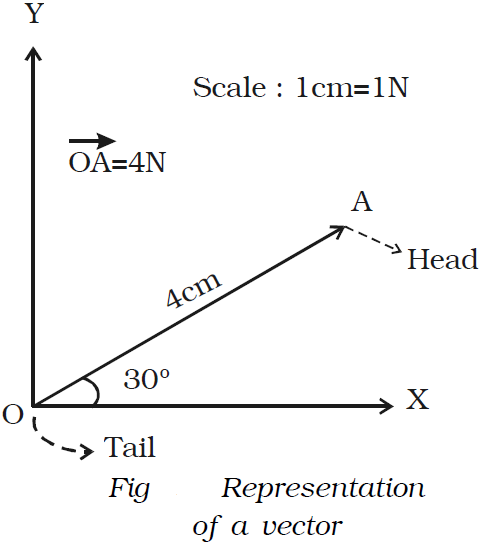
From the figure, it is clear that
● The scale is listed.
● A line with an arrow is drawn in a specified direction.
● The magnitude and direction of the vector are clearly labelled. In the above case, the diagram shows that the magnitude is 4 N and direction is 30° to x-axis. The length of the line gives the magnitude and arrow head gives the direction. In notation, the vector is denoted in bold face letter such as A or with an arrow above the letter as →A, read as vector A or A vector while its magnitude is denoted by A or by |A| .

Different types of vectors
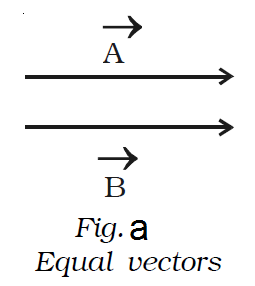
Equal vectors
Two vectors are said to be equal if they have the same magnitude and same direction, wherever be their initial positions. In Fig. a the vectors →A and →B have the same magnitude and direction. Therefore →A and →B are equal vectors.

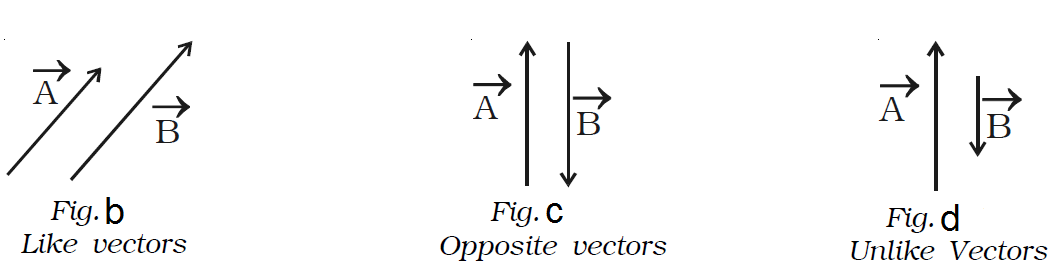
Like vectors
Two vectors are said to be like vectors, if they have same direction but different magnitudes as shown in Fig. b.

Opposite vectors
The vectors of same magnitude but opposite in direction, are called opposite vectors (Fig. c).

Unlike vectors
The vectors of different magnitude acting in opposite directions are called unlike vectors. In Fig. d the vectors →A and →B are unlike vectors.

Unit vector
A vector having unit magnitude is called a unit vector. It is also defined as a vector divided by its own magnitude. A unit vector in the direction of a vector →A is written as ^A and is read as ‘A cap’ or ‘A caret’ or ‘A hat’. Therefore, A
A^ = A→/|A→| (or) →A = ^A |→A|
Thus, a vector can be written as the product of its magnitude and unit vector along its direction.

Orthogonal unit vectors
There are three most common unit vectors in the positive directions of X,Y and Z axes of Cartesian coordinate system, denoted by i, j and k respectively. Since they are along the mutually perpendicular directions, they are called orthogonal unit vectors.

Null vector or zero vector
A vector whose magnitude is zero, is called a null vector or zero vector. It is represented by →0 and its starting and end points are the same. The direction of null vector is not known.

Proper vector
All the non-zero vectors are called proper vectors.

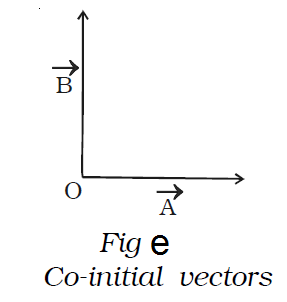
Co-initial vectors
Vectors having the same starting point are called co-initial vectors. In Fig. e, →A and →B start from the
same origin O. Hence, they are called as co-initial vectors.

 

 

 

Coplanar vectors
Vectors lying in the same plane are called coplanar vectors and the plane in which the vectors lie are called plane of vectors.

Addition of vectors
As vectors have both magnitude and direction they cannot be added by the method of ordinary algebra.
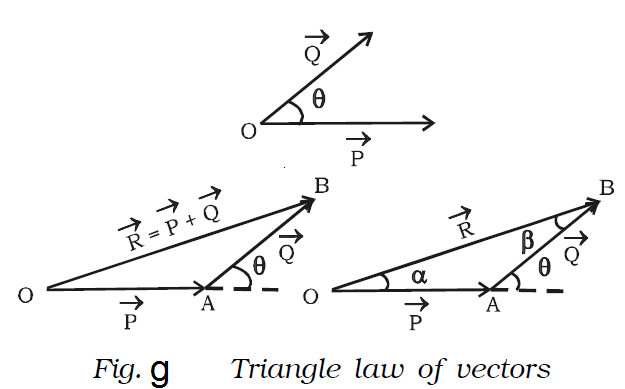
Vectors can be added graphically or geometrically. We shall now discuss the addition of two vectors graphically using head to tail method.
Consider two vectors →P and →Q which are acting along the same line. To add these two vectors, join the tail of
→Q with the head of →P (Fig. f).

The resultant of →P and →Q is →R = →P+→Q. The length of the line AD gives the magnitude of →R. →R acts in the same direction as that of →P and →Q.
In order to find the sum of two vectors, which are inclined to each other, triangle law of vectors or parallelogram law of vectors, can be used.

 

 

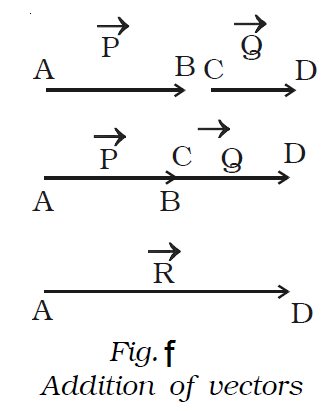
Triangle law of vectors
If two vectors are represented in magnitude and direction by the two adjacent sides of a triangle taken in order, then their resultant is the closing side of the triangle taken in the reverse order.

To find the resultant of two vectors →P and →Q which are acting at an angle θ, the following procedure is adopted.
First draw O A =→P (Fig. g) Then starting from the arrow head of →P, draw the vector =AB Q. Finally, draw a vector OB = →R from the
tail of vector →P to the head of vector →Q . Vector = OB R is the sum of the vectors →P and → Q. Thus →R = →P + →Q.

The magnitude of →P + →Q is determined by measuring the length of →R and direction by measuring the angle between →P and → R.
The magnitude and direction of →R , can be obtained by using the sine law and cosine law of triangles. Let α be the angle made by the resultant →R with →P . The magnitude of →R is,

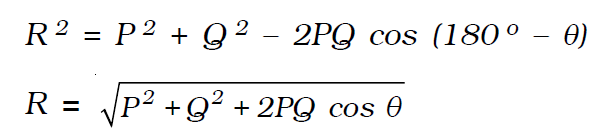
The direction of R can be obtained by,

 

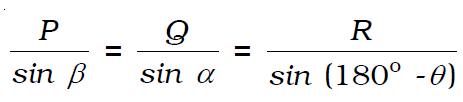
Parallelogram law of vectors
If two vectors acting at a point are represented in magnitude and direction by the two adjacent sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal passing through the common tail of the two vectors.

Let us consider two vectors →P and →Q which are inclined to each other at an angle θ as shown in Fig. h. Let the vectors →P and →Q be represented in magnitude and direction by the two sides OA and OB of a parallelogram OACB. The diagonal OC passing through the common tail O, gives the magnitude and direction of the resultant →R.
CD is drawn perpendicular to the extended OA, from C. Let COD made by → R with →P be α.

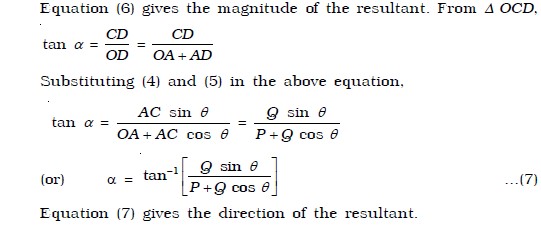
Special Cases
When two vectors act in the same direction
In this case, the angle between the two vectors θ = 0o, cos 0o = 1, sin 0o= 0

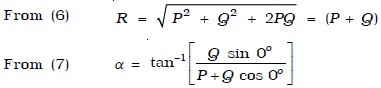
(i.e) α = 0
Thus, the resultant vector acts in the same direction as the individual vectors and is equal to the sum of the magnitude of the two vectors.

When two vectors act in the opposite direction

In this case, the angle between the two vectors θ = 180°, cos 180° = -1, sin 180o = 0.

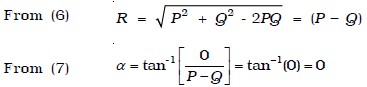
Thus, the resultant vector has a magnitude equal to the difference in magnitude of the two vectors and acts in the direction of the bigger of the two vectors

When two vectors are at right angles to each other
In this case, θ = 90°, cos 90o = 0, sin 90o = 1

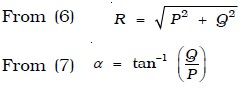
The resultant →R vector acts at an angle α with vector →P.

Subtraction of vectors
The subtraction of a vector from another is equivalent to the addition of one vector to the negative of the other.
For example →Q – →P = →Q + (-→P).
Thus to subtract →P from →Q , one has to add – →P with →Q (Fig i(a)). Therefore, to subtract →P from →Q , reversed →P is added to the → Q.

For this, first draw →AB = →Q and then starting from the arrow head of →Q , draw BC = (−→P) and finally join the head of – →P. Vector →R is the sum of → Q and – →P . (i.e) difference →Q – →P.

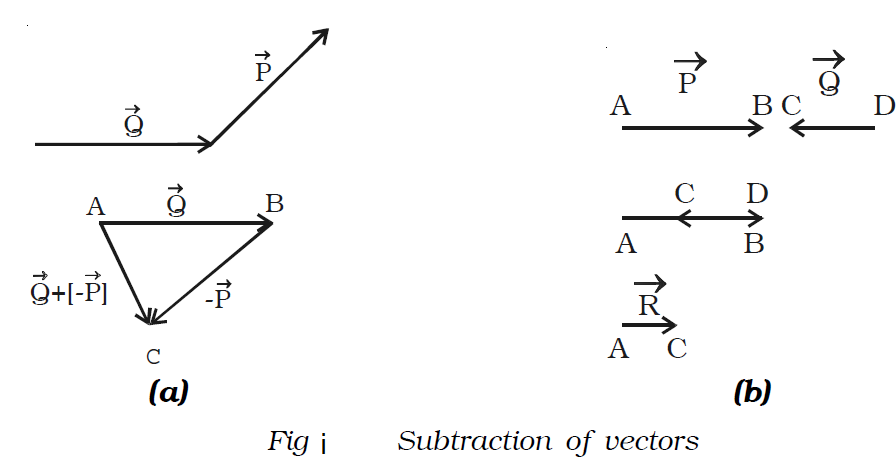
The resultant of two vectors which are anti-parallel to each other is obtained by subtracting the smaller vector from the bigger vector as shown in Fig i(b). The direction of the resultant vector is in the direction of the bigger vector.

Product of a vector and a scalar
Multiplication of a scalar and a vector gives a vector quantity which acts along the direction of the vector.
Examples
● If →a is the acceleration produced by a particle of mass m under the influence of the force, then →F = m→a
● momentum = mass × velocity (i.e) →P = m→v.

Resolution of vectors and rectangular components
A vector directed at an angle with the co-ordinate axis, can be resolved into its components along the axes. This process of splitting a vector into its components is known as resolution of a vector.
Consider a vector R = OA→ making an angle θ with X – axis. The vector R can be resolved into two components along X – axis and Y-axis respectively. Draw two perpendiculars from A to X and Y axes respectively. The intercepts on these axes are called the scalar components Rx and Ry.
Then, OP is Rx, which is the magnitude of x component of R→ as Ry, which is the magnitude of y component of →.R

Multiplication of two vectors
Multiplication of a vector by another vector does not follow the laws of ordinary algebra. There are two types of vector multiplication (i) Scalar product and (ii) Vector product.

Scalar product or Dot product of two vectors
If the product of two vectors is a scalar, then it is called scalar product. If → A and →B are two vectors, then their scalar product is written as → A. →B and read as → A dot →B. Hence scalar product is also called dot product. This is also referred as inner or direct product.

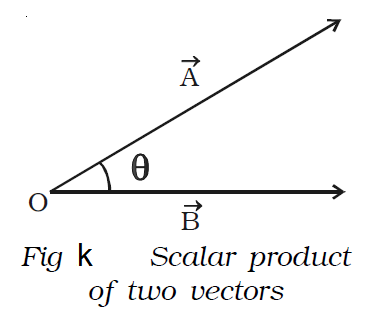
The scalar product of two vectors is a scalar, which is equal to the product of magnitudes of the two vectors and the cosine of the angle between them. The scalar product of two vectors → A and →B may be expressed as → A . →
B = |→A| |→B| cos θ where |→A| and |→B| are the magnitudes of →A and → B respectively and θ is the angle between →A and →B as shown in Fig k.

Vector product or Cross product of two vectors
If the product of two vectors is a vector, then it is called vector product. If →A and →B are two vectors then their vector product is written as →A × →B and read as →A cross →B. This is also referred as outer product.
The vector product or cross product of two vectors is a vector whose magnitude is equal to the product of their magnitudes and the sine of the smaller angle between them and the direction is perpendicular to a plane containing the two vectors.
If θ is the smaller angle through which →A should be rotated to reach →B, then the cross product of →A and →B (Fig. l) is expressed as,
→A × →B = |→A| |→B| sin θ ^n = →C

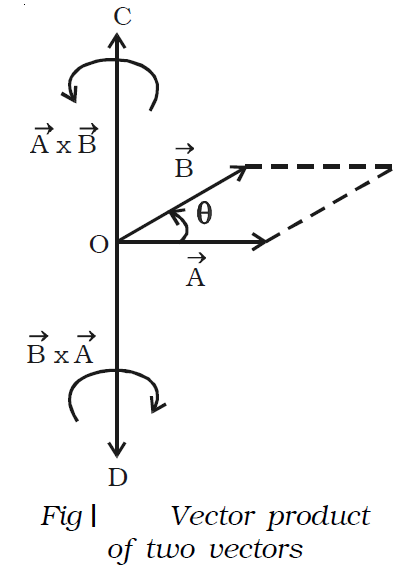
where |→A| and |→B| are the magnitudes of →A and →B respectively. →C is perpendicular to the plane containing → A and →B . The direction of →C is along the direction in which the tip of a screw moves when it is rotated from →A to →B. Hence →C acts along OC. By the same argument, →B × →A acts along OD.