Intermolecular forces
The force between two molecules of a substance is called intermolecular force. This intermolecular force is basically electric in nature. When the distance between two molecules is greater, the distribution of charges is such that the mean distance between opposite charges in the molecule is slightly less than the distance between their like charges. So a force of attraction exists. When the intermolecular distance is less, there is overlapping of the electron clouds of the molecules resulting in a strong repulsive force. The intermolecular forces are of two types. They are ▸ cohesive force and ▸ adhesive force.

Cohesive force
Cohesive force is the force of attraction between the molecules of the same substance. This cohesive force is very strong in solids, weak in liquids and extremely weak in gases.
Adhesive force
Adhesive force is the force of attraction between the moelcules of two different substances. For example due to the adhesive force, ink sticks to paper while writing. Fevicol, gum etc exhibit strong adhesive property. Water wets glass because the cohesive force between water molecules is less than the adhesive force between water and glass molecules. Whereas, mercury does not wet glass because the cohesive force between mercury molecules is greater than the adhesive force between mercury and glass molecules.

Molecular range and sphere of influence
Molecular range is the maximum distance upto which a molecule can exert force of attraction on another molecule. It is of the order of 10–9 m for solids and liquids. Sphere of influence is a sphere drawn around a particular molecule as centre and molecular range as radius. The central molecule exerts a force of attraction on all the molecules lying within the sphere of influence.

Surface tension of a liquid
Surface tension is the property of the free surface of a liquid at rest to behave like a stretched membrane in order to acquire minimum surface area.

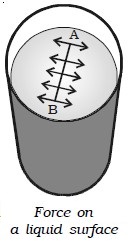
Imagine a line AB in the free surface of a liquid at rest (Fig. above). The force of surface tension is measured as the force acting per unit length on either side of this imaginary line AB. The force is perpendicular to the line and tangential to the liquid surface. If F is the force acting on the length l of the line AB, then surface tension is given by T = F/l.  Surface tension is defined as the force per unit length acting perpendicular on an imaginary line drawn on the liquid surface, tending to pull the surface apart along the line. Its unit is N m–1 and dimensional formula is MT–2.
Experiments to demonstrate surface tension
● When a painting brush is dipped into water, its hair gets separated from each other. When the brush is taken out of water, it is observed that its hair will cling together. This is because the free surface of water films tries to contract due to surface tension.

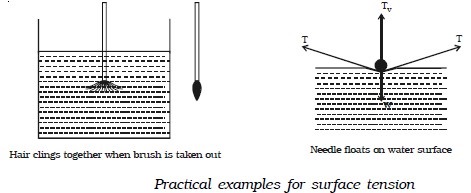
● When a sewing needle is gently placed on water surface, it floats. The water surface below the needle gets depressed slightly. The force of surface tension acts tangentially. The vertical component of the force of surface tension balances the weight of the needle.

Molecular theory of surface tension
Consider two molecules P and Q as shown in Fig. below. Taking them as centres and molecular range as radius, a sphere of influence is drawn around them.

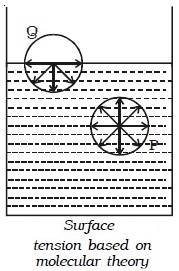
The molecule P is attracted in all directions equally by neighbouring molecules. Therefore net force acting on P is zero. The molecule Q is on the free surface of the liquid. It experiences a net downward force because the number of molecules in the lower half of the sphere is more and the upper half is completely outside the surface of the liquid. Therefore all the molecules lying on the surface of a liquid experience only a net downward force. If a molecule from the interior is to be brought to the surface of the liquid, work must be done against this downward force. This work done on the molecule is stored as potential energy. For equilibrium, a system must possess minimum potential energy. So, the free surface will have minimum potential energy. The free surface of a liquid tends to assume minimum surface area by contracting and remains in a state of tension like a stretched elastic membrane.

Surface energy and surface tension
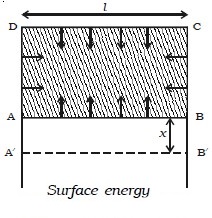
The potential energy per unit area of the surface film is called surface energy. Consider a metal frame ABCD in which AB is movable. The frame is dipped in a soap solution. A film is formed which pulls AB inwards due to surface tension. If T is the surface tension of the film and l is the length of the wire AB, this inward force is given by 2 × T l . The number 2 indicates the two free surfaces of the film. If AB is moved through a small distance x as shown in Fig. below to the position A B′ ′,
then work done is W = 2Tlx
Work down per unit area = W/2lx
∴ Surface energy = T2lx/2lx
Surface energy = T
Surface energy is numerically equal to surface tension.

Angle of contact
When the free surface of a liquid comes in contact with a solid, it becomes curved at the point of contact. The angle between the tangent to the liquid surface at the point of contact of the liquid with the solid and the solid surface inside the liquid is called angle of contact. In Fig. below, QR is the tangent drawn at the point of contact Q. The angle PQR is called the angle of contact. When a liquid has concave meniscus, the angle of contact is acute. When it has a convex meniscus, the angle of contact is obtuse.

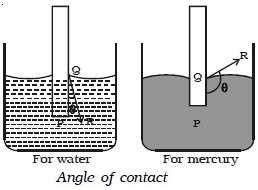
The angle of contact depends on the nature of liquid and solid in contact. For water and glass, θ lies between 8o and 18o. For pure water and clean glass, it is very small and hence it is taken as zero. The angle of contact of mercury with glass is 138o.

Pressure difference across a liquid surface
If the free surface of a liquid is plane, then the surface tension acts horizontally (Fig. below.a). It has no component perpendicular to the horizontal surface. As a result, there is no pressure difference between the liquid side and the vapour side.

If the surface of the liquid is concave (Fig. above.b), then the resultant force R due to surface tension on a molecule on the surface act vertically upwards. To balance this, an excess of pressure acting downward on the concave side is necessary. On the other hand if the surface is convex (Fig. above.c), the resultant R acts downward and there must be an excess of pressure on the concave side acting in the upward direction. Thus, there is always an excess of pressure on the concave side of a curved liquid surface over the pressure on its convex side due to surface tension.

Excess pressure inside a liquid drop
Consider a liquid drop of radius r. The molecules on the surface of the drop experience a resultant force acting inwards due to surface tension. Therefore, the pressure inside the drop must be greater than the pressure outside it. The excess of pressure P inside the drop provides a force acting outwards perpendicular to the surface, to balance the resultant force due to surface tension. Imagine the drop to be divided into two equal halves. Considering the equilibrium of the upper hemisphere of the drop, the upward force on the plane face ABCD due to excess pressure P is P π r 2 (Fig. below).

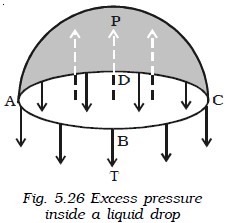
Consider a liquid drop of radius r. The molecules on the surface of the drop experience a resultant force acting inwards due to surface tension. Therefore, the pressure inside the drop must be greater than the pressure outside it. The excess of pressure P inside the drop provides a force acting outwards perpendicular to the surface, to balance the resultant force due to surface tension. Imagine the drop to be divided into two equal halves. Considering the equilibrium of the upper hemisphere of the drop, the upward force on the plane face ABCD due to excess pressure P is P π r 2 (Fig. above).
At equilibrium, Pπr 2 = T 2πr
∴ P = 2T/r

Excess pressure inside a soap bubble
A soap bubble has two liquid surfaces in contact with air, one inside the bubble and the other outside the bubble. Therefore the force due to surface tension = 2 × 2πrT
∴ At equilibrium, P πr 2 = 2 × 2πrT
(i.e) P = 4T/r
Thus the excess of pressure inside a drop is inversely proportional to its radius i.e. P α 1/r. As P α 1/r, the pressure needed to form a very small bubble is high. This explains why one needs to blow hard to start a balloon growing. Once the balloon has grown, less air pressure is needed to make it expand more.

Capillarity
The property of surface tension gives rise to an interesting phenomenon called capillarity. When a capillary tube is dipped in water, the water rises up in the tube. The level of water in the tube is above the free surface of water in the beaker (capillary rise). When a capillary tube is dipped in mercury, mercury also rises in the tube. But the level of mercury is depressed below the free surface of mercury in the beaker (capillary fall). The rise of a liquid in a capillary tube is known as capillarity. The height h in Fig. below indicates the capillary rise (for water) or capillary fall (for mercury).

Illustrations of capillarity
● A blotting paper absorbs ink by capillary action. The pores in the blotting paper act as capillaries.
● The oil in a lamp rises up the wick through the narrow spaces between the threads of the wick.
● A sponge retains water due to capillary action.
●Walls get damped in rainy season due to absorption of water by bricks.

Surface tension by capillary rise method
Let us consider a capillary tube of uniform bore dipped vertically in a beaker containing water. Due to surface tension, water rises to a height h in the capillary tube as shown in Fig. below. The surface tension T of the water acts inwards and the reaction of the tube R outwards. R is equal to T in magnitude but opposite in direction. This reaction R can be resolved into two rectangular components.

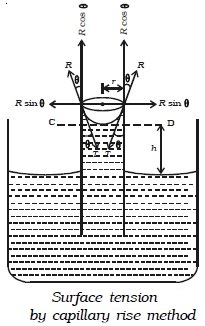
● Horizontal component R sin θ acting radially outwards
● Vertical component R cos θ acting upwards.
The horizontal component acting all along the circumference of the tube cancel each other whereas the vertical component balances the weight of water column in the tube.
Total upward force = R cos θ × circumference of the tube
(i.e) F = 2πr R cos θ or F = 2πr T cos θ …(1)
[∵ R = T ]
This upward force is responsible for the capillary rise. As the water column is in equilibrium, this force acting upwards is equal to weight of the water column acting downwards.
(i.e) F = W …(2)
Now, volume of water in the tube is assumed to be made up of (i) a cylindrical water column of height h and (ii) water in the meniscus above the plane CD.
Volume of cylindrical water column = πr2h
Volume of water in the meniscus = (Volume of cylinder of height r and radius r) – (Volume of hemisphere)

Experimental determination of surface tension of water by capillary rise method
A clean capillary tube of uniform bore is fixed vertically with its lower end dipping into water taken in a beaker. A needle N is also fixed with the capillary tube as shown in the Fig. below. The tube is raised or lowered until the tip of the needle just touches the water surface. A travelling microscope M is focussed on the meniscus of the

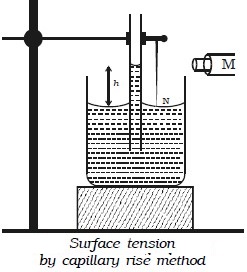
water in the capillary tube. The reading R1 corresponding to the lower meniscus is noted. The microscope is lowered and focused on the tip of the needle and the corresponding reading is taken as R2. The difference between R1 and R2 gives the capillary rise h. The radius of the capillary tube is determined using the travelling microscope. If ρ is the density of water then the surface tension of water is given by T = hrρg/2 where g is the acceleration due to gravity.

Factors affecting surface tension
Impurities present in a liquid appreciably affect surface tension. A highly soluble substance like salt increases the surface tension whereas sparingly soluble substances like soap decreases the surface tension. The surface tension decreases with rise in temperature. The temperature at which the surface tension of a liquid becomes zero is called critical temperature of the liquid.

Applications of surface tension
● During stormy weather, oil is poured into the sea around the ship. As the surface tension of oil is less than that of water, it spreads on water surface. Due to the decrease in surface tension, the velocity of the waves decreases. This reduces the wrath of the waves on the ship.
● Lubricating oils spread easily to all parts because of their low surface tension.
● Dirty clothes cannot be washed with water unless some detergent is added to water. When detergent is added to water, one end of the hairpin shaped molecules of the detergent get attracted to water and the other end, to molecules of the dirt. Thus the dirt is suspended surrounded by detergent molecules and this can be easily removed.
This detergent action is due to the reduction of surface tension of water when soap or detergent is added to water.
●Cotton dresses are preferred in summer because cotton dresses have fine pores which act as capillaries for the sweat.