Torque
Torque is the turning moment of a force. When a force produces the rotation of a body without translation motion, there must be a second force acting upon the body equal and  opposite to the first so that the resultant force is zero. That is, the forces are in equilibrium. Consider the spanner and nut shown in Fig. 1(a). When a force F₁ is applied to the end of the spanner, an equal and opposite parallel force F₂ occurs at the nut. If this were not so, there would be motion of translation in the direction of force F₁. When two equal and opposite forces act on a body they are said to form a couple.

Torque (T ) = magnitude of the applied force (F₁) × length of the torque arm (d)

Where:

T = torque (Nm)

F = force (N) and d = moment arm (m)

 

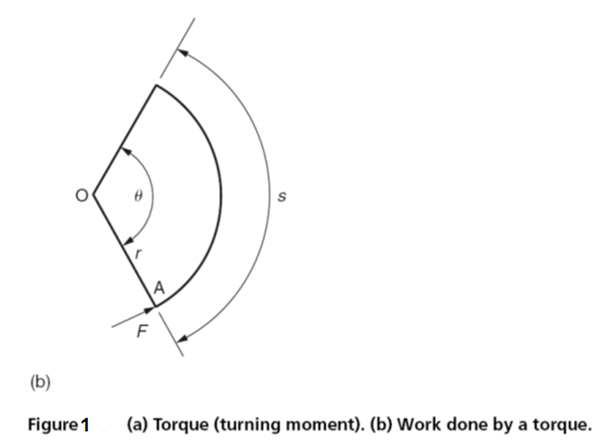
Work done by a torque
Consider the work done by a force F (N) acting at right angles to the moment arm OA of length r (m) and rotating through an angle θ rad as shown in Fig. 1(b).

Work done = linear distance moved by a force = s × F (Nm or J)

But:
s = rθ (m)

Therefore:
work done = rθ × F = Fr ×θ

But:
torque T = Fr

Therefore:
work done =Tθ (Nm or J)

Work done by a torque = torque × angle of rotation in radians
 

Example
A flywheel rotates at 2400 rev/min. It is suddenly subjected to a breaking torque which results in an angular retardation (deceleration) of 10 m/s². Calculate:

(a) the time taken to slow the flywheel down to 600 rev/min;
(b) the angular velocity of the flywheel after it has rotated through 300 revolutions from the start of its deceleration.
(a) Apply the equation:

ω ₂ = ω ₁ + α t

Where:

ω ₁ = initial angular velocity = (2400 rev/min × 2π) /60 rad/s
ω ₂ = angular velocity after time t = (600 × 2π)/60 rad/s
α= angular acceleration =-10 m/s² (the minus sign indicates a deceleration)

Therefore:
(600 × 2 π)/60 = (2400 rev/min × 2 π)/60 + (-10)t

10t = (1800 ×  2 π)/60

Therefore:
t = 18.8 s

 (b) Apply equation:

(ω ₂)² = (ω ₁)² + 2 αθ

Where:
ω ₂ = angular velocity after rotating through 300 rev
ω ₁ = (2400 rev/min ×  2 π )/60 rad/s = 251.33 rad/s

α=-10 rad/s²
θ=300 ×  2 π rad

Then:

ω ₂ ² = 251.332 + 2 × (-10) × 600 π
=63166.8 – 37699.1
= 159.6 rad/s or

= (159.6 × 60)/2 π
=1524 rev/min