A liquid in motion possesses pressure energy, kinetic energy and potential energy.

Pressure energy
It is the energy possessed by a liquid by virtue of its pressure. Consider a liquid of density ρ contained in a wide tank T having a side tube near the bottom of the tank as shown in Fig. below. A frictionless piston of cross sectional area ‘a’ is fitted to the side tube. Pressure exerted by the liquid on the piston is P = h ρ g where h is the height of liquid column above the axis of the side tube.
If x is the distance through which the piston is pushed inwards, then
Volume of liquid pushed into the tank = ax
∴ Mass of the liquid pushed into the tank = ax ρ
As the tank is wide enough and a very small amount of liquid is pushed inside the tank, the height h and hence the pressure P may be considered as constant.
Work done in pushing the piston through the distance x = Force on the piston × distance moved
(i.e) W = Pax
This work done is the pressure energy of the liquid of mass axρ.
∴ Pressure energy per unit mass of the liquid = Pax/axρ =P/ρ

Kinetic energy
It is the energy possessed by a liquid by virtue of its motion.
If m is the mass of the liquid moving with a velocity v, the kinetic energy of the liquid = 1/2 mv2.
Kinetic energy per unit mass = 1/2mv2/m =v2/2

Potential energy
It is the energy possessed by a liquid by virtue of its height above the ground level.
If m is the mass of the liquid at a height h from the ground level, the potential energy of the liquid = mgh
Potential energy per unit mass = mgh/m = gh
Total energy of the liquid in motion = pressure energy + kinetic energy + potential energy.
∴ Total energy per unit mass of the flowing liquid = P/ρ + v2/2 + gh

Equation of continuity
Consider a non-viscous liquid in streamline flow through a tube AB of varying cross section as shown in Fig. below Let a1 and a2 be the
area of cross section, v1 and v2 be the velocity of flow of the liquid at A and B respectively.

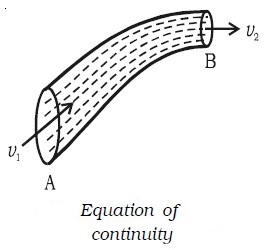
∴ Volume of liquid entering per second at A = a1v1.
If ρ is the density of the liquid, then mass of liquid entering per second at A = a1v1ρ.
Similarly, mass of liquid leaving per second at B = a2v2ρ
If there is no loss of liquid in the tube and the flow is steady, then mass of liquid entering per second at A = mass of liquid leaving per
second at B
(i.e) a1v1ρ = a2v2ρ or a1v1 = a2v2
i.e. av = constant
This is called as the equation of continuity. From this equation v α 1/a.
i.e. the larger the area of cross section the smaller will be the velocity of flow of liquid and vice-versa.

Bernoulli’s theorem
In 1738, Daniel Bernoulli proposed a theorem for the streamline flow of a liquid based on the law of conservation of energy. According to Bernoulli’s theorem, for the streamline flow of a non-viscous and incompressible liquid, the sum of the pressure energy, kinetic energy and
potential energy per unit mass is a constant.

(i.e) P/ρ + v2/2 + gh = constant
This equation is known as Bernoulli’s equation.
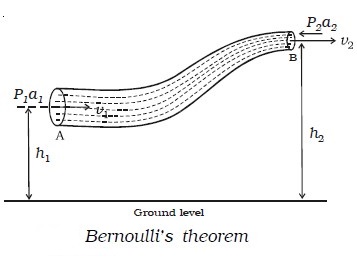
Consider streamline flow of a liquid of density ρ through a pipe AB of varying cross section. Let P1 and P2 be the pressures and a1 and a2, the cross sectional areas at A and B respectively. The liquid enters A normally with a velocity v1 and leaves B normally with a velocity v2. The liquid is accelerated against the force of gravity while flowing from A to B, because the height of B is greater than that of A from the ground level. Therefore P1 is greater than P2. This is maintained by an external force. The mass m of the liquid crossing per second through any section of the tube in accordance with the equation of continuity is
a1v1ρ = a2v2ρ = m
or a1v1 = a2v2 = m/ρ = V …(1)
As a1 > a2 , v1 < v2
The force acting on the liquid at A = P1a1
The force acting on the liquid at B = P2 a2
Work done per second on the liquid at A = P1a1 × v1 = P1V
Work done by the liquid at B = P2a2 × v2 = P2V
∴ Net work done per second on the liquid by the pressure energy in moving the liquid from A to B is = P1V – P2V …(2)
If the mass of the liquid flowing in one second from A to B is m, then increase in potential energy per second of liquid from A to B is
mgh2 – mgh1
Increase in kinetic energy per second of the liquid

Special case :
If the liquid flows through a horizontal tube, h1 = h2. Therefore there is no increase in potential energy of the liquid i.e. the gravitational head becomes zero.
∴ equation (3) becomes
P/ρ + 1/2 v2 = a constant
This is another form of Bernoulli’s equation.

Application of Bernoulli’s theorem
Lift of an aircraft wing
A section of an aircraft wing and the flow lines are shown in Fig. below. The orientation of the wing relative to the flow direction causes
the flow lines to crowd together above the wing. This corresponds to increased velocity in this region and hence the pressure is reduced. But below the wing, the pressure is nearly equal to the atmospheric pressure. As a result of this, the upward force on the underside of the wing is greater than the downward force on the topside. Thus there is a net upward force or lift.

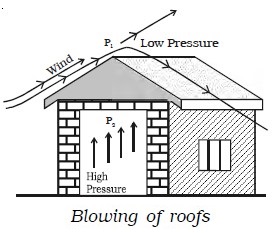
Blowing of roofs
During a storm, the roofs of huts or tinned roofs are blown off without any damage to other parts of the hut. The blowing wind creates a low pressure P1 on top of the roof. The pressure P2 under the roof is however greater than P1. Due to this pressure difference, the roof is lifted and blown off with the wind.

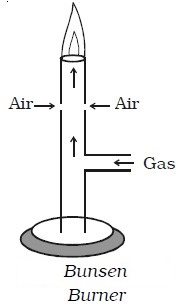
Bunsen burner
In a Bunsen burner, the gas comes out of the nozzle with high velocity. Due to this the pressure in the stem of the burner decreases. So, air from the atmosphere rushes into the burner.

Motion of two parallel boats
When two boats separated by a small distance row parallel to each other along the same direction, the velocity of water between the boats becomes very large compared to that on the outer sides. Because of this, the pressure in between the two boats gets reduced. The high pressure on the outer side pushes the boats inwards. As a result of this, the boats come closer and may even collide.