Trigonometric formulae – Basic definitions 

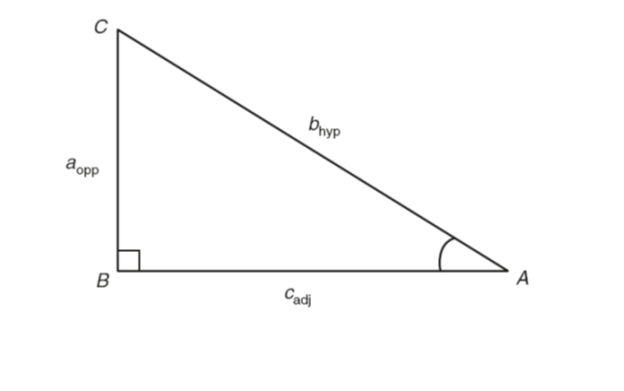
Trigonometric formulae – In the right-angled triangle shown below, a is the side opposite to angle A, b is the hypotenuse of the triangle and c is the side adjacent to angle A. By definition:

SinA=opp/hyp=a/b

cosA=adj/hyp=c/b

tanA=opp/adj=a/c

cosecA=hyp/opp=b/a=1/sinA

secA=hyp/adj=b/c=1/cosA

cotA=adj/opp=c/a=1/tanA

Identities

sin²A+cos²A=1

1 +tan²A= sec²A

1 +cot²A =cosec²A

sin(-A) =-sin A

cos(-A)=cos A

tan(-A)=-tan A

 

Compound and double angle formulae

sin(A+B)= sinA cos B+cos A sin B

sin(A –B)=sinA cos B-cos A sin B

cos(A+B)=cos A cos B-sinA sin B

cos(A –B) =cos A cos B+sinA sin B

tan(A+B)=(tanA +tan B)/(1-tan A tan B)

tan(A–B)=(tanA -tan B)/(1+tan A tan B)

sin 2A =2 sinA cos A

cos 2A=  cos²A -sin²A= 2 cos²A -1=1 -2 sin²A

tan 2A =(2 tan A)/(1-tan²A)

 

‘Product to sum’ formulae

sinAcosB=1/2[sin(A+B)+sin(A-B)]

cosAsinB=1/2[sin(A+B)-sin(A-B)]

cosAcosB=1/2[cos(A+B)+cos(A-B)]

sinAsinB=-1/2[cos(A+B)-cos(A-B)]

 

Triangle formulae

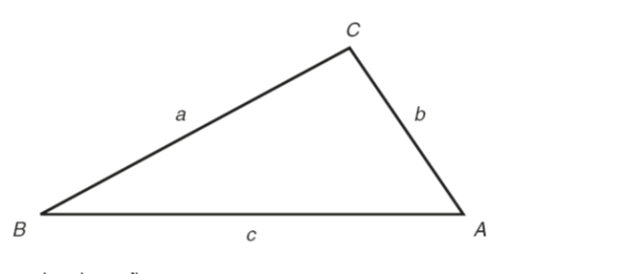
With reference to the above figure:

Sine rule:

a/sinA= b/sin B= c/sin C

Cosine rule:

a² =b² +c² -2bc cos A

b²=c² +a² -2ca cos B

c²=a²+b² -2ab cos C

Area:

Area=1/2ab sin C=1/2 bc sinA =1/2ca sin B

Also

Area=√s(s-a)(s-b)(s-c)

 where: s is the semi-perimeter, that is, (a+b+c)/2