The revolution of the Earth around the Sun, rotating fly wheel, electrons revolving around the nucleus, spinning top, the motion of a fan blade, revolution of the moon around the Earth etc. are some examples of circular motion. In all the above cases, the bodies or particles travel in a circular path. So, it is necessary to understand the motion of such bodies. When a particle moves on a circular path with a constant speed, then its motion is known as uniform circular motion in a plane. The magnitude of velocity in circular motion remains constant but the direction changes continuously.

Let us consider a particle of mass m moving with a velocity v along the circle of radius r with centre O as shown in Fig above. P is the position of the particle at a given instant of time such that the radial line OP makes an angle θ with the reference line DA. The magnitude of the velocity remains constant, but its direction changes continuously. The linear velocity always acts tangentially to the position of the particle (i.e) in each position, the linear velocity →v is perpendicular to the radius vector →r.

Angular displacement
Let us consider a particle of mass m moving along the circular path of radius r as shown in Fig. below. Let the initial position of the particle be A. P and Q are the positions of the particle at any instants of time t and t + dt respectively. Suppose the particle traverses a distance ds along the circular path in time interval dt. During this interval, it moves through an angle dθ = θ2 − θ1. The angle swept by the radius vector at a given time is called the angular displacement of the particle.

If r be the radius of the circle, then the angular displacement is given by dθ = rds. The angular displacement is measured in terms of radian.

Angular velocity
The rate of change of angular displacement is called the angular velocity of the particle. Let dθ be the angular displacement made by the particle in time dt , then the angular velocity of the particle is dt dθ ω = . Its unit is rad s– 1 and dimensional formula is T–1.
For one complete revolution, the angle swept by the radius vector is 360o or 2π radians. If T is the time taken for one complete revolution, known as period, then the angular velocity of the particle is T2 t θ π ω = = .

Relation between linear velocity and angular velocity

Angular acceleration
If the angular velocity of the body performing rotatory motion is non-uniform, then the body is said to possess angular acceleration. The rate of change of angular velocity is called angular acceleration. The angular acceleration is measured in terms of rad s−2 and its dimensional formula is T − 2.

Centripetal acceleration
The speed of a particle performing uniform circular motion remains constant throughout the motion but its velocity changes continuously due to the change in direction (i.e) the particle executing uniform circular motion is said to possess an acceleration. Consider a particle executing circular motion of radius r with linear velocity v and angular velocity ω. The linear velocity of the particle acts along the tangential line. Let dθ be the angle described by the particle at the centre when it moves from A to B in time dt. The velocity v at B of the particle makes an angle dθ with the line BC and hence it is resolved horizontally as v cos dθ along BC and vertically as v sin d θ along BD.At A and B, linear velocity v acts along AH and BT respectively. ∠AOB = dθ = ∠HET (∵ angle subtended by the two radii of a circle = angle subtended by the two tangents).

∴ The change in velocity along the horizontal direction = v cos dθ −v If dθ is very small, cos dθ = 1
∴ Change in velocity along the horizontal direction = v − v = 0
(i.e) there is no change in velocity in the horizontal direction.

The change in velocity in the vertical direction (i.e along AO) is
dv = v sin dθ − 0 = v sin dθ
If dθ is very small, sin dθ = dθ

Centripetal force
According to Newton’s first law of motion, a body possesses the property called directional inertia (i.e) the inability of the body to change its direction. This means that without the application of an external force, the direction of motion can not be changed. Thus when a body is moving along a circular path, some force must be acting upon it, which continuously changes the body from its straight-line path (Fig below). It makes clear that the applied force should have no component in the direction of the motion of the body or the force must act at every
point perpendicular to the direction of motion of the body. This force, therefore, must act along the radius and should be directed towards the centre.

Hence for circular motion, a constant force should act on the body, along the radius towards the centre and perpendicular to the velocity of the body. This force is known as centripetal force. If m is the mass of the body, then the magnitude of the centripetal force is given by F = mass × centripetal acceleration. = m (v2/r) = mv2/r = m(rw2)

Examples
Any force like gravitational force, frictional force, electric force, magnetic force etc. may act as a centripetal force. Some of the examples of centripetal force are :
● In the case of a stone tied to the end of a string whirled in a circular path, the centripetal force is provided by the tension in the string.
● When a car takes a turn on the road, the frictional force between the tyres and the road provides the centripetal force.
● In the case of planets revolving round the Sun or the moon revolving round the earth, the centripetal force is provided by the gravitational force of attraction between them.
● For an electron revolving round the nucleus in a circular path, the electrostatic force of attraction between the electron and the nucleus provides the necessary centripetal force.

Centrifugal reaction
According to Newton’s third law of motion, for every action there is an equal and opposite reaction. The equal and opposite reaction to the centripetal force is called centrifugal reaction, because it tends to take the body away from the centre. In fact, the centrifugal reaction is a pseudo or apparent force, acts or assumed to act because of the acceleration of the rotating body. In the case of a stone tied to the end of the string is whirled in a circular path, not only the stone is acted upon by a force (centripetal force) along the string towards the centre, but the stone also exerts an equal and opposite force on the hand (centrifugal force) away from the centre, along the string. On releasing the string, the tension disappears and the stone flies off tangentially to the circular path along a straight line as enuciated by Newton’s first law of motion. When a car is turning round a corner, the person sitting inside the car experiences an outward force. It is because of the fact that no centripetal force is supplied by the person. Therefore, to avoid the outward force, the person should exert an inward force.

Applications of centripetal forces
Motion in a vertical circle
Let us consider a body of mass m tied to one end of the string which is fixed at O and it is moving in a vertical circle of radius r about the point O as shown in Fig. below. The motion is circular but is not uniform, since the body speeds up while coming down and slows down while going up.

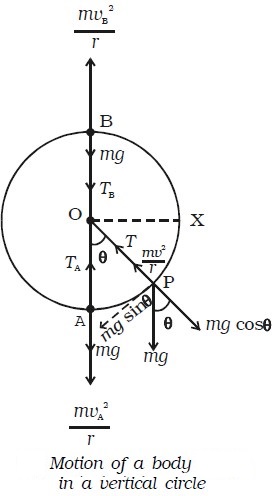
Suppose the body is at P at any instant of time t, the tension T in the string always acts towards 0.
The weight mg of the body at P is resolved along the string as mg cos θ which acts outwards and mg sin θ, perpendicular to the string.
When the body is at P, the following forces acts on it along the string.
● mg cos θ acts along OP (outwards)
● tension T acts along PO (inwards)
Net force on the body at P acting along PO = T – mg cos θ
This must provide the necessary centripetal force mv2/r.
Therefore, T – mg cos θ = mv2/r
T = mg cos θ + mv2/r …(1)

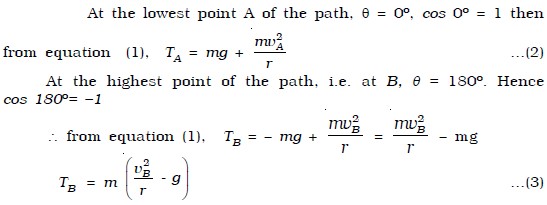
If TB > 0, then the string remains taut while if TB < 0, the string slackens and it becomes impossible to complete the motion in a vertical circle. If the velocity vB is decreased, the tension TB in the string also decreases, and becomes zero at a certain minimum value of the speed called critical velocity. Let vC be the minimum value of the velocity, then at vB = vC , TB = 0. Therefore from equation (3),

The velocity vA of the body at the bottom point A can be obtained by using law of conservation of energy. When the stone rises from A to B, i.e through a height 2r, its potential energy increases by an amount equal to the decrease in kinetic energy. Thus, (Potential energy at A + Kinetic energy at A ) = (Potential energy at B + Kinetic energy at B)


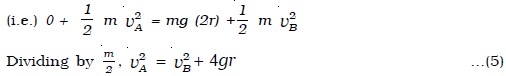
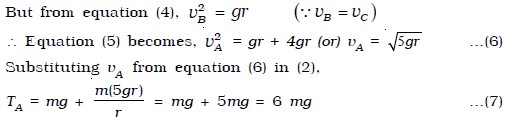
While rotating in a vertical circle, the stone must have a velocity greater than 5gr or tension greater than 6mg at the lowest point, so that its velocity at the top is greater than gr or tension > 0. An aeroplane while looping a vertical circle must have a velocity greater than 5gr at the lowest point, so that its velocity at the top is greater than gr. In that case, pilot sitting in the aeroplane will not fall.

Motion on a level circular road
When a vehicle goes round a level curved path, it should be acted upon by a centripetal force. While negotiating the curved path, the wheels of the car have a tendency to leave the curved path and regain the straight-line path. Frictional force between the tyres and the road opposes this tendency of the wheels. This frictional force, therefore, acts towards the centre of the circular path and provides the necessary centripetal force.

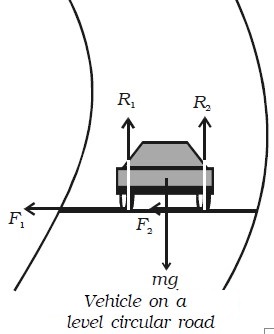
In Fig. above, weight of the vehicle mg acts vertically downwards. R1, R2 are the forces of normal reaction of the road on the wheels. As the road is level (horizontal), R1, R2 act vertically upwards. Obviously,
R1 + R2 = mg …(1)
Let μ * be the coefficient of friction between the tyres and the road, F1 and F2 be the forces of friction between the tyres and the road, directed towards the centre of the curved path.
∴ F1 = μR1 and F2 = μR2 …(2)

Banking of curved roads and tracks
When a car goes round a level curve, the force of friction between the tyres and the road provides the necessary centripetal force. If the frictional force, which acts as centripetal force and keeps the body moving along the circular road is not enough to provide the necessary centripetal force, the car will skid. In order to avoid skidding, while going round a curved path the outer edge of the road is raised above the level of the inner edge. This is known as banking of curved roads or tracks.

Bending of a cyclist round a curve
A cyclist has to bend slightly towards the centre of the circular track in order to take a safe turn without slipping. Fig. below shows a cyclist taking a turn towards his right on a circular path of radius r. Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle θ. Let R be the reaction

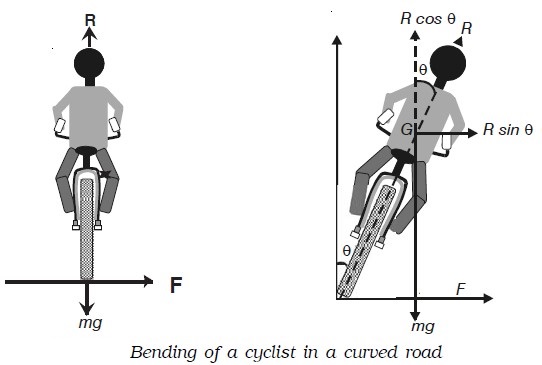
of the ground on the cyclist. The reaction R may be resolved into two components: (i) the component R sin θ, acting towards the centre of the curve providing necessary centripetal force for circular motion and (ii) the component R cos θ, balancing the weight of the cyclist along with the bicycle.

For small values of θ, sin θ = tan θ
Therefore from equations (3) and (4)
tan θ = h/l = v2/rg …(5)
Obviously, a road or track can be banked correctly only for a particular speed of the vehicle. Therefore, the driver must drive with a particular speed at the circular turn. If the speed is higher than the desired value, the vehicle tends to slip outward at the turn but then the frictional force acts inwards and provides the additional centripetal force. Similarly, if the speed of the vehicle is lower than the desired speed it tends to slip inward at the turn but now the frictional force acts outwards and reduces the centripetal force.

Condition for skidding
When the centripetal force is greater than the frictional force, skidding occurs. If μ is the coefficient of friction between the road and tyre, then the limiting friction (frictional force) is f = μR where normal reaction R = mg
∴f = μ (mg)
Thus for skidding, Centripetal force > Frictional force

(i.e) when the tangent of the angle of banking is greater than the coefficient of friction, skidding occurs.