Learn about Variation of acceleration due to gravity

Variation of g with altitude
Let P be a point on the surface of the Earth and Q be a point at an altitude h. Let the mass of the Earth be M and radius of the Earth be R. Consider the Earth as a spherical shaped body.

Variation of g with depth
Consider the Earth to be a homogeneous sphere with uniform density of radius R and mass M. Let P be a point on the surface of the Earth and Q be a point at a depth d from the surface.

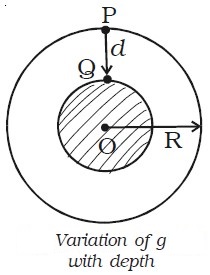
The acceleration due to gravity at P on the surface is g = GM/R2.
If ρ be the density, then, the mass of the Earth is M = 4/3 π R3ρ

Variation of g with latitude (Non−sphericity of the Earth)
The Earth is not a perfect sphere. It is an ellipsoid as shown in the Fig. below. It is flattened at the poles where the latitude is 90o and bulged at the equator where the latitude is 0o.

The radius of the Earth at equatorial plane Re is greater than the radius along the poles Rp by about 21 km.
We know that g = GM/R2
∴ g α 1/R2
The value of g varies inversely as the square of radius of the Earth. The radius at the equator is the greatest. Hence the value of g is minimum at the equator. The radius at poles is the least. Hence, the value of g is maximum at the poles. The value of g increases from the equator to the poles.

Variation of g with latitude (Rotation of the Earth)
Let us consider the Earth as a homogeneous sphere of mass M and radius R. The Earth rotates about an axis passing through its north and south poles. The Earth rotates from west to east in 24 hours. Its angular velocity is 7.3 × 10−5 rad s−1. Consider a body of mass m on the surface of the Earth at P at a latitude θ. Let ω be the angular velocity. The force (weight) F = mg acts along PO. It could be resolved into two rectangular components (i) mg cos θ along PB and (ii) mg sin θ along PA (Fig. below).

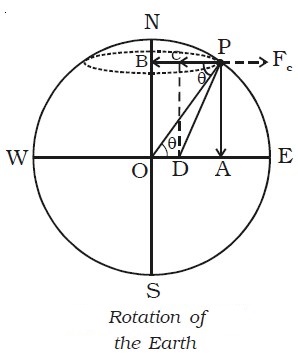
From the ΔOPB, it is found that BP = R cos θ. The particle describes a circle with
B as centre and radius BP = R cos θ.
The body at P experiences a centrifugal force (outward force) FC due to the rotation of the Earth.
(i.e) FC = mRω2 cos θ .
The net force along PC = mg cos θ − mRω2 cos θ
∴ The body is acted upon by two forces along PA and PC.