The terms work and energy are quite familiar to us and we use them in various contexts. In everyday life, the term work is used to refer to any form of activity that requires the exertion of mental or muscular efforts. In physics, work is said to be done by a force or against the direction of the force, when the point of application of the force moves towards or against the direction of the force. If no displacement takes place, no work is said to be done. Therefore for work to be done, two essential conditions should be satisfied:

● a force must be exerted
● the force must cause a motion or displacement

If a particle is subjected to a force F and if the particle is displaced by an infinitesimal displacement ds , the work done dw by the force is dw = →F . →ds.

Work is a scalar quantity and has magnitude but no direction.

The work done by a force when the body is displaced from position P to P1 can be obtained by integrating the above equation,

W = ∫ dw = ∫ (F cos θ ) ds

Work done by a constant force
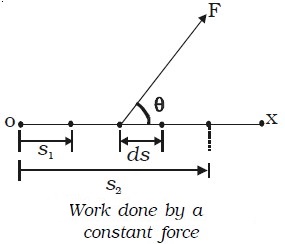
When the force F acting on a body has a constant magnitude and acts at a constant angle θ from the straight line path of the particle as shown in image below, then,


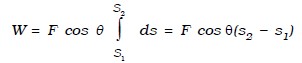
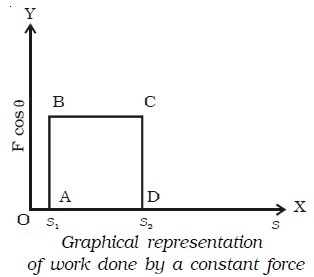
The graphical representation of work done by a constant force is shown in image below.
W = F cos θ (s2–s1) = area ABCD

Work done by a variable force
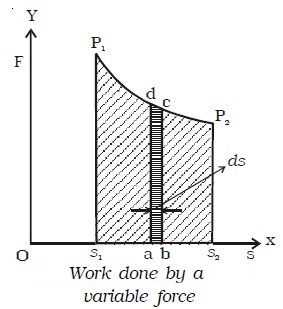
If the body is subjected to a varying force F and displaced along X axis as shown in Fig below,

work done dw = F cos θ. ds = area of the small element abcd.

Therefore, the total work done when the body moves from s1 to s2 is Σ dw= W = area under the curve P1P2 = area S1 P1 P2 S2

The unit of work is joule. One joule is defined as the work done by a force of one newton when its point of application moves by one metre along the line of action of the force.

Special cases
● When θ = 0 , the force F is in the same direction as the displacement s.
∴ Work done, W = F s cos 0 = F s

● When θ = 90°, the force under consideration is normal to the direction of motion.
∴Work done, W = F s cos 90° = 0

For example, if a body moves along a frictionless horizontal surface, its weight and the reaction of the surface, both normal to the surface, do no work. Similarly, when a stone tied to a string is whirled around in a circle with uniform speed, the centripetal force continuously changes the direction of motion. Since this force is always normal to the direction of motion of the object, it does no work.

● When θ = 180°, the force F is in the opposite direction to the displacement.
∴ Work done (W) = F s cos 180°= −F s
(eg.) The frictional force that slows the sliding of an object over a surface does a negative work. A positive work can be defined as the work done by a force and a negative work as the work done against a force.